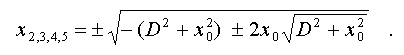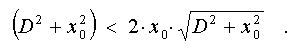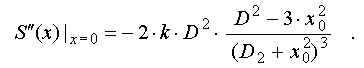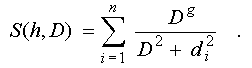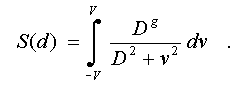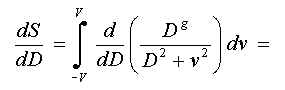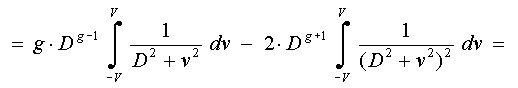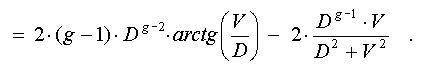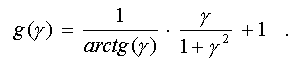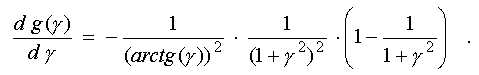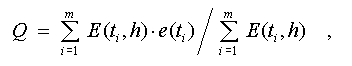APPENDIX
1.6.A. Estimation of the Bell-Approximation Resolution.
Let's consider the simplest case of two parallel segments placed on
distance 2*x_0 from each other. The cross-section of the considered picture
is shown on fig.5a. On this picture the position of the approximating
segment axial line is determined by parameter x. In this case
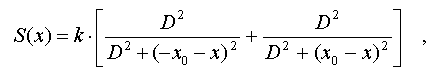
Where k - number
of points in each segment.
Extrema of such
measure are determined by zero values of its derivative:
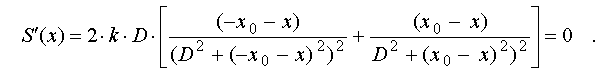
The denominator
of resulting expression is positive at any values of entering variables.
The numerator can be transformed to the view
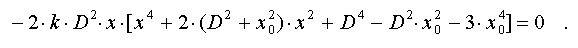
This equation
has five solutions, one of which is x_1 = 0, and four others :
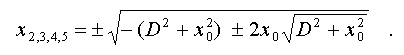
Two solutions
which are determined by a difference of the expressions placed under
sign of exterior square root, have imaginary values at any values of
entering variables (as x_0> 0, under the initial agreement - see fig.5a).
Others two have real values, when
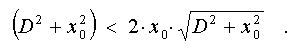
Simplifying this
expression, we shall obtain that at D < sqrt(3)*x_0 investigated conformity
function has three extremums: one central and two symmetric side ones. It
is easy to show, that:
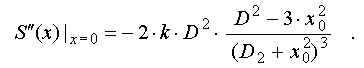
It is obvious,
if D < sqrt(3)*x_0, then S"(x)|_0 > 0, i.e. the central extremum
is a local minimum of considered conformity function of and, hence,
adjacent side exremums are local maximums of this function (see fig.5b).
At D > sqrt(3)*x_0, these maximums merge in one (see fig.5c). Positions
of maximums depending on a value of parameter D are shown on fig.5d
(see the formula for an evaluation of x_2... x_5).
1.7.A. Adding to
the Problem of the Automatic Correction of the Width of the Membership Function.
As it is affirmed,
the maximum of the function of conformity that is determined by expression
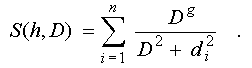
is reached at
the finite value of parameter D, when the exponent in which it is raised
in numerator - g (governing the amplitude growth rate) lays in the interval
1 < g < 2.
Let's prove this
statement.
Let's consider
an approximated segment (see fig.6b) as a continuous point set. In this
case the conformity measure is determined by an integral
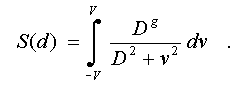
Here the variable
v = d is entered to avoid confusion with differential label. The behaviour
of this measure depending on width of membership functions is defined
by a derivative on D:
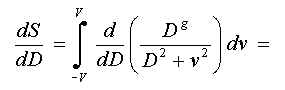
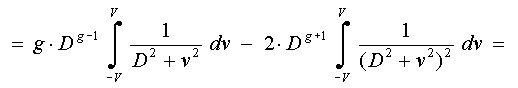
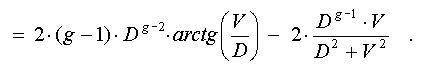
Equating this
expression to zero, and introducing the variable gamma = V/D, we obtain:
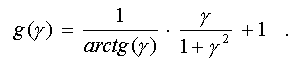
In a range of
interest for us (0 < gamma < oo) this function has the maximum value
2 at gamma = 0 and asymptotically comes nearer to 1 at gamma -> oo
(see fig.6d).
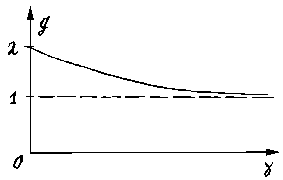
|
Fig.6d
|
Its decrease
monotonicity is confirmed by that its derivative everywhere is negative
in the interval 0 < gamma < oo:
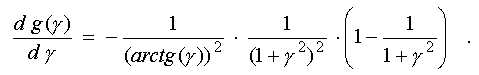
A graph of the inverse function
D/V=1/gamma (g), our actual subject of interest, is represented on fig.6c.
This graph shows, what will be the width of memberships functions (in
comparison with the flowing relative width of the approximated segment)
at reaching by the considered conformity measure of its maximum value depending
on index g, governing amplitude growth rate of memberships functions.
2.2.A. Choice of
the Step of the Start Positions for the Procedure of the Contour Boundary
Representation in Terms of the Contiguous Segments.
A beforehand
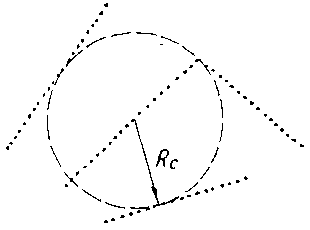
value of the least radius of neighbourhoods R_min among radii of neighbourhoods
R_c of all contour segments of the treated image was estimated. The radius
of the neighbourhood is a radius of the greatest circle with the center
on the given segment, intercrossed by it and not containing points of other
segments (fig.27).
|
Fig.27
|
Parameters of
X, Y initial sets were defined by nodes of some grid on the image plane.
Density of the grid was chosen so that in any circle in radius R_min/2 one
node of this grid hitted even. In the case of a square grid its step should
be less, than R_min/sqrt(2). Remaining parameters were prescribed identical
to all sets. A value of parameter B corresponding to length of initial
contiguous segments was chosen smaller than (R_min/2)*sqrt(3). This choice
is caused by the obtained theoretical estimation for a resolving power
of the suggested approximation method. Parameter D was chosen equal 0.5*B,
A - arbitrary, P1 = P2 = 0.
2.2.B. Particularities
of the Gradiet Procedure of the Local Maximum Detection of the Bell-Conformity.
During the given work several gradient procedures of search of local
extremums have been tested. Their principal means consist in deployment
of the frame corresponding to displacement of the central point of an
approximating segment, along ridges of the conformity function. A characteristic
example - the procedure circumscribed in [34].
However, use of such universal (that is why rather bulky) procedures
does not justify itself in a situation when the preliminary count of
specificity of the variables is possible,that simplifies extremum search.
Specificity of the variables consists here in their well defined hierarchy.
First of all the angle and cross position of a contiguous segment are
arranged, a after them - parameters of branches. And only then moving in
the longitudinal direction is carried out.
Such specificity
of variables has allowed to use effectively at the second stage of
experiments the gradient procedure in which moving on all variables
of eight-parametrical conformity measure is carried out simultaneously
and basically is independent. During searching delays are possible
(misses of steps on some variables) if parameters with higher priority
were not arranged yet. In final variant the following system of priorities
was used: (+, A), (P1, P2), (D), (B1, B2, =) where - "+" and "=" designate
moving in cross and longitudinal directions accordingly. The step on
any variable increases half (with the count of restriction on maximum
value - see further) if the it is executed in the same direction, as previous,
and decreases otherwise. Thus it is considered, that those variables
were arranged, the step on which became less, than 1/4 from the maximum
admissible value on the given variable.
The last values
were chosen from the most common reasons so that as a result of each
step the new approximating segment not too overstepped the bounds of
old onethe. Steps in a longitudinal direction (and on length of the branches)
were limited to value B/2, and in cross - D/2. Steps on the angle and
curvature should not oscillate ends of the segment on value bigger than
D/2, i.e.  A*MAX(B1, B2)/0.7 and
A*MAX(B1, B2)/0.7 and  P * (B/0.7)/2 should not exceed D/2. In order to prevent discretization
disclosures of analysed contours, the value of parameter D was limited
from below to the value ranging 0.5 - 2.5 distances between adjacent points
of the raster. From above parameter D was limited by value B/2.
P * (B/0.7)/2 should not exceed D/2. In order to prevent discretization
disclosures of analysed contours, the value of parameter D was limited
from below to the value ranging 0.5 - 2.5 distances between adjacent points
of the raster. From above parameter D was limited by value B/2.
Particularly
such restrictions are organized so, that at the approach to one of them
it is authorized to make the following step only on half of the distance
before this restriction. It simply enough ensures a possibility of increase
of a step if a necessity of movement in the opposite direction exists.
Initial steps on separate components were chosen equal to the half of
their greatest possible values. Thus initial values of parameters B and
D were accepted equal 10 and 4 accordingly, and as much as the possible
admissible step value on D equal 0.5. Search procedure of the next conformity
measure maximum stopped when steps on all variables became smaller, than
0.2 of their maximum possible admissible values.
As a rule, search of the maximums
corresponding to contour segments required on the average 60-80 steps
on theof declination angle and position in the cross direction at 8-12
steps in the longitudinal direction.
2.2.C. Estimation of quality - filling ratio
of contiguous segments.
The property
of filling ratio of a resulting segment is defined as follows:
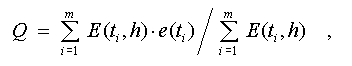
Where
t_1, t_2... t_m
- coordinates of points of the raster;
E (t_i, h) -
|
membership function which is determined
by parameters of the found maximum
(h = {X, Y, A, D, P1, P2, B1, B2});
|
e (t_i) -
|
the indicator function marking contour
points:
=
1 if the given raster point is included into the number of contour
points;
=
0, otherwise.
|
In the first
series of experiments those segments were only considered acceptable
which have filling ratio over 0.5.
According to sparsed representation,
the filling ratio criterion of contiguous segments was modified also.
The essence of such modification consists in the following. The axial
line of a tested segment is divided into the intervals equal to a step
of tracking of contour boundaries. Within the limits of each interval there
is the contour point nearest to the axial line. Values of memberships
functions to these points are summarized, and the obtained outcome is divided
on the greatest possible value of this sum when within the limits of each
interval there is a point laying on the segment axial line. In the second
series of experiments the segments which filling ratio exceeded 0.8 were
considered as acceptable ones.
2.2.D. Additional
techniques.
To
avoid a repeated finding of segments and to simplify searching less expressed
maximums,
the
contour points laying inside the image piece corresponding the found segment,
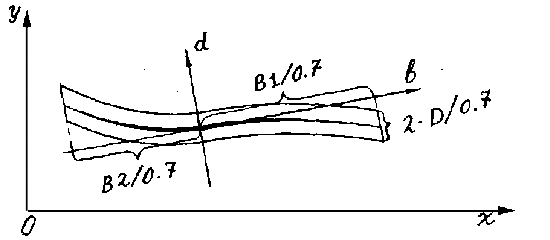
were excluded from the further reviewing. Each of such pieces represents
a corridor in width 2D/0.7, enclosing the axial line of the given segment;
length of branches of this corridor - B1/0.7 and B2/0.7 (fig.9).
|
Fig.9
|
To avoid superfluous losses
of time, the operation of rough choice of the contour points concerning
to the flowing contiguous segment was applied. In the beginning for an
evaluation of coincidence measure gradient of chosen contour points (the
list of references to their initial set is formed) which lay inside a
wide rectangle enclosing the contiguous segment in its flowing position
(such neighbourhood is shown by fat primes on fig.12).
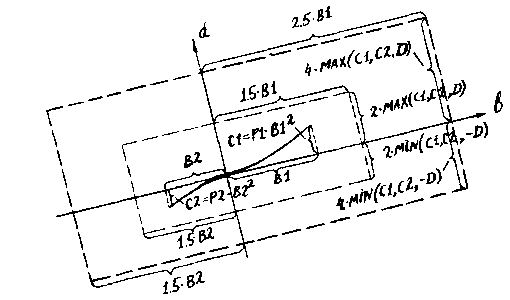
|
Fig.12
|
Further, on each step a
possibility of build-up of new, narrower neighbourhood for a flowing
position of the contiguous segment (thin primes on fig.12), not passing
out of former wide neighbourhood is checked. If it is impossible, a list
of references is made on a new wide neighbourhood.
Operations
of deletion and preliminary choice have not only engineering sense.
A solution of basic problems depends on their organization too. In particular,
ability of the procedure to understand complicated situations depends
on their organization, - at processing of false concentrations of
contour points, in the case of capture of several segments. In similar
cases the number of steps noticeably increased (sometimes so, that it was
necessary to discontinue compulsorily process of searching). Detection
of such situations was carried out by criterion of filling ratio of resulting
segments by contour points. An example of such situation is shown on fig.11.
On this picture it is shown the initial (dotted line) and finite (solid
line) positions of the contiguous segment, corresponding to process of search
of one local maximum. Apparently, the right branch of the initial contiguous
segment has not had time to be rounded along the corresponding piece
of the contour line and intersected an adjacent contour.
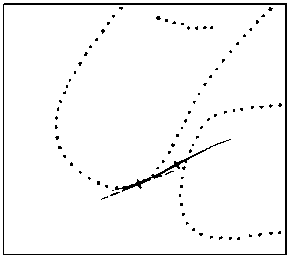
|
Fig.11
|
Thus it is obvious, that
deletion of the piece of image corresponding to the finite position of
such segment is wrongful. The contiguous segments started from other initial
positions can correctly interpret an observed picture. The solution accepted
in this occasion is based on this reason. The elementary contours laying
in a neighbourhood of the contour movement from which led to an unacceptable
segment, were excluded from candidates in initial approximations. So the
situation shown on fig.11, for example, was treated - as an initial approximation
the elementary segment was chosen, the distance from which up to an outside
contour exceeded the corresponding distance for the initial segment which
had led to false outcome.
This
example illustrates common logic of solution of complicated situations.
To solve them it is necessary to begin from the outside - from
the "free" ends of entering lines.
3.5.A. Some Details
of the Procedure of the Accumulation of the Hypotheses.
In
the program realizing hypotheses accumulation procedure information only
about the marked zones is stored. For this purpose some array is assigned,
the entry in which is made with help of L-hashing [35]
at which zone number is a key, and the hashing function is a remainder of
division of zone number on array size. In the carried out experiments this
array consisted of 4096 cells. Thus the initial search address of the cell
corresponding to a zone with given number (hashing function) was obtained
by zeroing of top digits of this number (since 13-th). In each cell, except
for a zone key (number in a common hypothetical three-dimensional array of
the zones), a reference to a description of the given zone is stored. The
zone description too is one cell of some array in which the bites are marked
corresponding to numbers of those hypograms which marked the given zone. Thus
the zone mark with a separate hypogram is reduced to logic addition of its
descriptions to the cell in which bite is marked that corresponds to the
current hypogram number(an array of such cells is prepared beforehand). After
the termination of marking process with all hypograms, operation of transformation
of contents of each description into number of hypograms which marked it
(for each description it is one machine command by estimation of units in
the given cell) is started.
At execution
of smoothing procedure numbers of neighboring zones are not calculated anew
but d are calculated by addition to components translating the number
of the central zone into number of one of 27 adjacent zones (3x3x3). These
components are calculated beforehand. The logic of their evaluation is
defined by logic of an evaluation of common linear number of an element
(zone) in a multivariate (three-dimensional) array.
To reduce number of contiguous segments
tracing a reference contour at build-up of its hypogram, the next reference
hypogram points are under construction on a forward branch of last contiguous
segment. It is possible to tell, that on this branch the fictitious tangential
contiguous segment moves ahead, and in its frame positions of the basis vector
are registered. The boundary of such construction is defined by mismatch of
positions of the basis vector in frames of actual and fictitious segments.
Thus a movement step of actual segments is continuously arranged with the
help of feed-back so that to keep the mismatch value within the limits of
a zone quarter, and a step of fictitious segments have to keep adjacent points
of the reference hypogram within the limits of one zone. The zone, as well
as earlier, is meant as an element of subdivision of parametrical space.
If it is not possible to be made, it is accepted, that in this place the
hypogram has a rupture and its construction proceeds from other place of
the standard contour.
3.5.B. Illustration
rationality of smoothing operation.
|
Fig.26
|
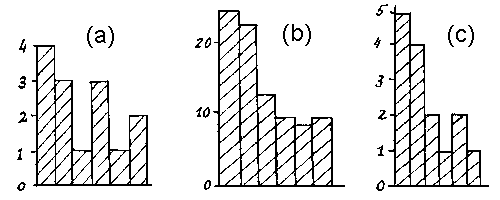
The initial histogram of
the most powerful cluster (fig.24a and fig.26b) is shown on fig.26a. Here
weight of the zone is a number of hypograms marking its. Rationality of
smoothing operation in this case is confirmed by a view of the initial histogram
of the same cluster at size of zones reduced in one and a half time (fig.26c).
Thus also the centers of zones of the space of search parameters accordingly
have somewhat moved. This example shows that relatively big weight of
a collateral ejection (fig.26a) is caused, first of all, by accidents of
distribution of hypogram points within the limits of adjacent zones.
In [3]
the operation of multiple smoothing has been suggested. In this case smoothing
is done{made} iterativelly until the condition will be satisfied that
at two sequential stages the same zone (besides the unique one) has the
maximum sum (among all zones at the given stage). The center of this zone
is accepted as a search cluster point. Though such the procedure has not
shown crucial advantages in comparison with once made smoothing, it is
expedient to have its in a collection of tools of the analysis of hypogram
intersection. Multiple smoothing will coordinate a cluster point (zone) with
its environment. If this point is on a cluster boundary it is gradually shifted
in its center. The stability of this point (zone) at several sequential
stages of smoothing is some performance of its common reliability. Besides,
if the cluster top is not acute, i.e. consists of several zones that (due
to the count of neighboring zones) one zone of maximum weight will be allocated
which position will depend on a context (i.e. weightinesses of enclosing
zones).
In last version of program realization
of hypotheses accumulation process an attempt has been undertaken to limit
an amount of the zones participating in the subsequent procedure of smoothing.
For this purpose so-called areas of intersection were selected, which represent
set of the zones marked more than two hypograms, and also one time marked
zones directly adjoining to this set (the neighbourhood, as well as earlier,
the nearest 3*3*3). However, in spite of the fact that, for example in
the circumscribed experiment, execution time of the smoothing procedure
on the average was reduced with 1.5 up to 0.5 s, it was additionally required
about 0.5 s for detection of these areas (thus the number of analysed
zones was reduced on the average in 5 times). Probably, this procedure will
have essential advantages at more rigid restrictions on entrance in an
area of intersection. Naturally, the operation of restriction of number
of analysed zones has an essential importance at multiply repeated smoothing.
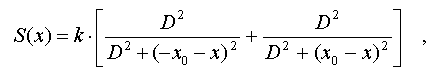
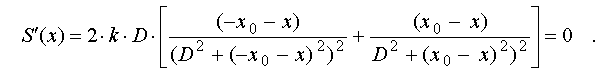
![]()