| Russian |
1.7.A. Adding to the Problem of the
Automatic Correction of the Width of the Membership Function.
As it is affirmed,
the maximum of the function of conformity that is determined by expression
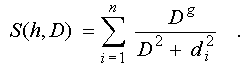
is reached at
the finite value of parameter D, when the exponent in which it is raised
in numerator - g (governing the amplitude growth rate) lays in the interval
1 < g < 2.
Let's prove this
statement.
Let's consider
an approximated segment (see fig.6b) as a continuous point set. In this
case the conformity measure is determined by an integral
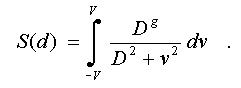
Here the variable
v = d is entered to avoid confusion with differential label. The behaviour
of this measure depending on width of membership functions is defined
by a derivative on D:
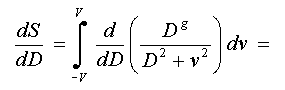
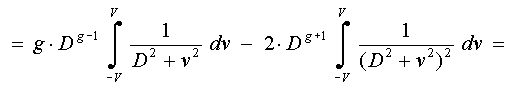
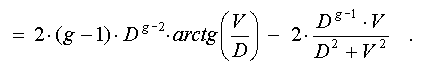
Equating this
expression to zero, and introducing the variable gamma = V/D, we obtain:
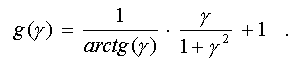
In a range of
interest for us (0 < gamma < oo) this function has the maximum value
2 at gamma = 0 and asymptotically comes nearer to 1 at gamma -> oo
(see fig.6d).
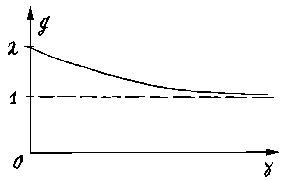
|
| Fig.6d |
Its decrease
monotonicity is confirmed by that its derivative everywhere is negative
in the interval 0 < gamma < oo:
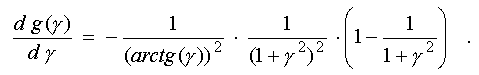
A graph of the
inverse function D/V=1/gamma (g), our actual subject of interest, is represented
on fig.6c. This graph shows, what will be the width of memberships functions
(in comparison with the flowing relative width of the approximated segment)
at reaching by the considered conformity measure of its maximum value
depending on index g, governing amplitude growth rate of memberships functions.