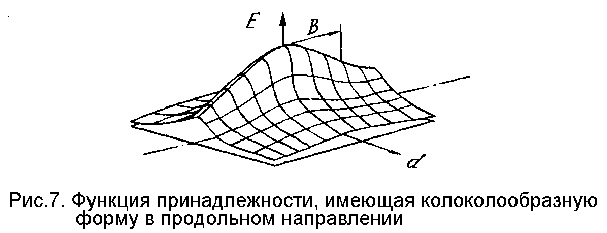
2. ПРЕДСТАВЛЕНИЕ КОНТУРНЫХ ГРАНИЦ В ТЕРМИНАХ ПРИЛЕГАЮЩИХ ОТРЕЗКОВ

К выводу о целесообразности использования такой функции принадлежности приводит и тот факт, что не существует ограниченного набора кривых какого-либо стандартного типа, способных исчерпать все многообразие форм криволинейных отрезков криволинейной - плавной - формы. "Лекалами-эталонами" такие отрезки описываются только приблизительно. Здесь также естественно потребовать максимального приближения аппроксимирующего ("эталонного") отрезка по центру с возможностью постепенного ослабления этого "приближения" к периферии.

Эти соображения и легли в основу предлагаемого метода описания контурных границ в терминах отрезков с нечеткими концами. В проведенных исследованиях в качестве осевых линий аппроксимирующих отрезков использовались кривые простейшего аналитического типа, а именно - центральные участки парабол. Причем каждая ветвь могла иметь свою кривизну. Для подстройки длины ветвей использовался механизм, аналогичный подстройке ширины отрезков. Мера сходства, построенная в соответсви с этими соображениями, имеет следующее математическое выражение:

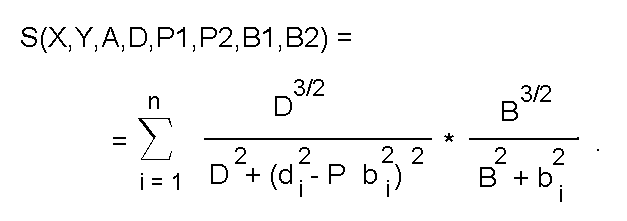
где b_i, d_i - параметры, задающие положение контурной точ- ки в собственной системе координат аппроксимирующего отрезка (рис.8); эти параметры определяются по координатам точки x_i, y_i с помощью преобразований

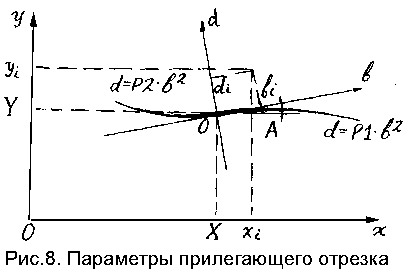
b_i = (x_i - X)*cos(A) + (y_i - Y)*sin(A),

d_i = -(x_i - X)*sin(A) + (y_i - Y)*cos(A);

X,Y - координаты центра отрезка;

A - угол наклона отрезка;

P = P1, если b_i >= 0 (кривизна правой ветви),

/ = P2, если b_i < 0 (кривизна левой ветви);

B = B1, если b_i >= 0 (длина правой ветви),

/ = B2, если b_i < 0 (длина левой ветви);

D - полуширина функции принадлежности.

Отрезки, отвечающие локальным максимумам такой меры сходства, должны в наибольшей степени соответствовать аппроксимируемым участкам своими центральными частями с постепенным ослаблением этого соответствия к периферии. В дальнейшем, следуя [3], будем называть такие отрезки прилегающими. На рис.8 символически показан отдельный прилегающий отрезок. Здесь уменьшение толщины отрезка соответствует уменьшению его четкости, т.е. степени соответствия аппроксимируемому контуру.

2.1. Результаты предварительных экспериментов

Программная реализация предлагаемого метода аппроксимации контурных границ была выполнена на языке ФОРТРАН-ДУБНА (небольшая часть - на автокоде МАДЛЕН). Эксперименты проводились на ЭВМ БЭСМ-6, к которой была подключена телевизионная камера (через 64-уровневый аналого-цифровой преобразователь). Производительность ЭВМ - 1 млн. опер./с, оперативная память - 32К слов по 48 разрядов.

Для поиска локальных максимумов рассмотренной восьмипараметрической меры сходства использовалась градиентная процедура с регулируемым шагом. Компоненты градиента вычислялись на основе аналитических выражений для частных производных.

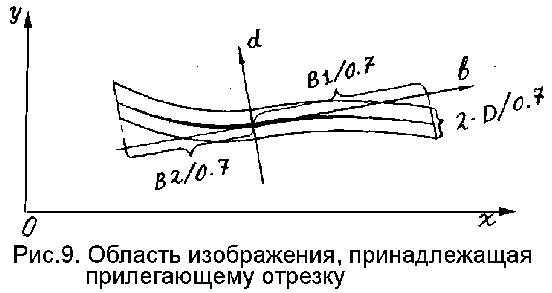
Чтобы избежать повторного нахождения отрезков и упростить поиск менее выраженных максимумов, контурные точки, лежащие внутри участка изображения, отвечающего очередному найденному отрезку, исключались из дальнейшего рассмотрения. Каждый из таких участков представляет коридор шириной 2D/0.7, окружающий осевую линию данного отрезка; длина ветвей этого коридора - B1/0.7 и B2/0.7 (рис.9).

На рис.10а показаны контурные границы одного из реальных изображений, используемых в первой серии экспериментов. Размер исходного полутонового изображения - 290 х 196 точек. Всего на изображении получено около 800 контурных точек, т.е. точек растра, через которые проходили элементарные контуры, выделенные оператором Хюккеля [5,6]. Начальные положения прилегающих отрезков задавались в узлах регулярной прямоугольной сетки с шагом 12 точек растра исходного изображения (соображения, на основе которых выбирался этот шаг, приведены в Приложении 3). Начальные значения остальных параметров принимались следующими: B1 = B2 = 5, D = 2.5, A = 0, P1 = P2 = 0.

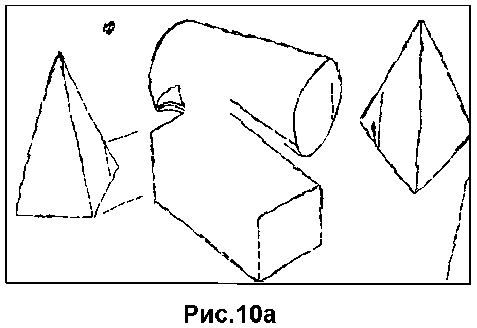
Как правило, каждый запуск градиентной процедуры, используемой для поиска локальных максимумов нечеткой меры сходства, приводил к нахождению истинного прилегающего отрезка (рис.10б).

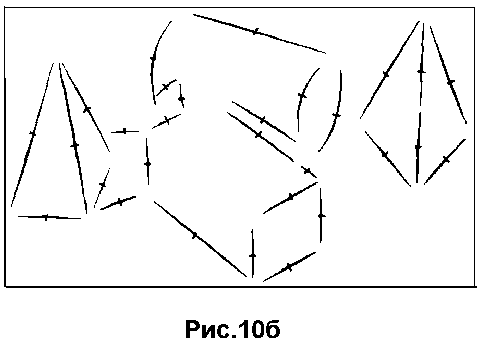
Выборка проверяемых ситуаций была достаточно представительной: запуск производился из 384 позиций, равномерно распределенных по приведенному изображению, представляющих самые различные взаимные положения начальных приближений и искомых отрезков. Не более 10 пусков привело к ошибочной аппроксимации: либо к "захвату" случайного скопления контурных точек, не похожего на отрезок линий ("пятну"), либо к "захвату" нескольких близко расположенных отрезков. Такие случаи определялись по явному нарушению процесса поиска - чрезмерному увеличению длины (ширины) получаемого отрезка или числа шагов, либо по критерию заполненности результирующего отрезка контурными точками:

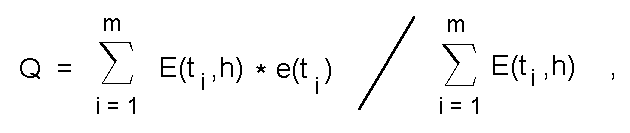
где t_1, t_2 ... t_m - координаты точек сетчатки (растра); E(t_i,h) - функция принадлежности, определяемая параметрами найденного максимума (h = {X,Y,A,D,P1,P2,B1,B2}); e(t_i) - индикаторная функция, отмечающая контурные точки:

     e(t_i) = 1, если данная точка сетчатки входит в число контурных точек;

            / = 0, в противном случае.

В дальнейшей работе учитывались только те отрезки, заполненность которых превышала 0.5.

Проведенные таким образом эксперименты показали, что максимумы, отвечающие искомым отрезкам, характеризуются гладкими склонами, поглощающими ложные максимумы. Предварительные эксперименты доказали принципиальную возможность получения описания контурных фигур в терминах прилегающих отрезков, соответствующих интуитивным представлениям.

2.2. Усовершенствование процедуры поиска локальных максимумов нечеткой меры сходства

Анализ поведения градиентной процедуры, первоначально используемой для поиска локальных максимумов нечеткой меры сходства [2], показал, что в окрестностях своих максимумов (т.е. на заключительных этапах поиска) функция сходства имеет вид длинных и узких хребтов, вытянутых вдоль осевых линий контурных границ. При этом аппроксимирующие отрезки могут долго колебаться в направлении, поперечном к этим линиям, с очень медленным продвижением в продольном направлении. Для быстрого прохождения этих хребтов в [3] было предложено смещать в процессе поиска центральную точку аппроксимирующего отрезка не по осям системы координат изображения, а вдоль и поперек текущего направления его осевой линии. Так как осевая линия аппроксимирующего отрезка постепенно подстраивается под осевую линию представляемого участка контурной границы, продольное движение отрезка осуществляется непосредственно вдоль осевой линии упомянутых хребтов. Такая организация процедуры поиска локальных максимумов меры сходства позволила довольно быстро и четко проходить вышеупомянутые хребты этой меры.

Сложности здесь возникали только на "ложных" скоплениях контурных точек, например, в случае "захвата" нескольких отрезков. В этих случаях число шагов заметно возрастало (иногда настолько, что приходилось принудительно останавливать процесс поиска). Выявление таких ситуаций осуществлялось по критерию заполненности результирующих отрезков контурными точками. На рис.11 приведен пример такой ситуации. На этом рисунке показано начальное (пунктиром) и конечное (сплошной линией) положения прилегающего отрезка, отвечающие процессу поиска одного локального максимума. Как видно, правая ветвь начального прилегающего отрезка не успела "закруглиться" вдоль соответствующего участка контурной линии и "перерезала" соседний контур.

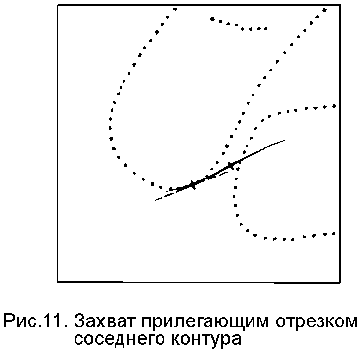
При этом очевидно, что вычеркивание участка изображения, отвечающего конечному положению такого отрезка, неправомерно, так как прилегающие отрезки, запущенные из других начальных положений, могут правильно проинтерпретировать наблюдаемую картину. Предлагаемое решение рассматриваемой проблемы основано именно на этом соображении. Элементарные контуры, лежащие в окрестности контура, движение от которого привело к неприемлемому отрезку, исключались из кандидатов в начальные приближения. Так, например, обрабатывалась ситуация, показанная на рис.11, - в качестве начального приближения выбирался элементарный отрезок, расстояние от которого до постороннего контура превышало соответствующее расстояние для начального отрезка, приведшего к ложному результату.

Для того чтобы избежать лишних потерь времени, при реализации процедуры описании контурных границ прилегающими отрезками применялась операция грубого выбора контурных точек, относящихся к текущему прилегающему отрезку. Вначале для вычисления градиента меры сходства выбираются контурные точки (формируется список ссылок на исходное их множество), которые лежат внутри широкого прямоугольника, окружающего прилегающий отрезок в его текущей позиции (такая окрестность показана жирными штрихами на рис.12).

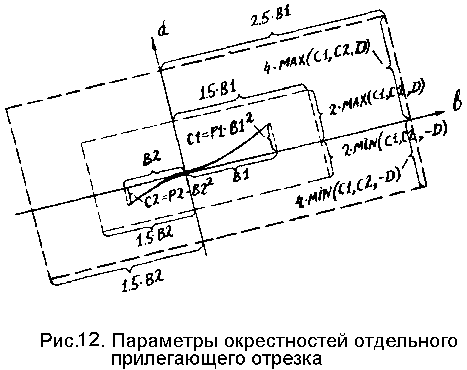
Далее на каждом шаге проверяется возможность построения новой, более "узкой" окрестности для текущего положения прилегающего отрезка (тонкие штрихи на рис.12), не выходящей за пределы прежней широкой окрестности. Если это невозможно, список ссылок пересоставляется по новой широкой окрестности.

В соответствии с рекомендациями, высказанными в разделе 1.2., процедура поиска прилегающих отрезков была "переведена" с растрового представления контуров, на их "прореженное" представление, точки которого определись центральными точками элементов контурных границ получаемых с помощью оператора Хюккеля. Кроме того, наиболее четкие элементы контура выделяемые с помощью этого оператора использовались в качестве начальных приближений для последующей процедуры поиска протяженных (прилегающих) отрезков (в первой серии экспериментов для этого использовались узлы регулярной сетки).

В соответствии с "прореженным" представлением был модифицирован и критерий заполненности прилегающих отрезков контурными точками. Суть такой модификации состоит в следующем. Осевая линия проверяемого отрезка разбивается на интервалы, равные шагу отслеживания контурных границ. В пределах каждого интервала находится контурная точка, ближайшая к осевой линии. Значения функции принадлежности в этих точках суммируются, и полученный результат делится на максимально возможную величину этой суммы, когда в пределах каждого интервала имеется точка, лежащая на осевой линии отрезка. В данной серии экспериментов приемлемыми считались отрезки, заполненность которых превышала 0.8.

На рис.13 показано контурное изображение, на котором проверялась работоспособность усовершенствованной процедуры представления контурных границ прилегающими отрезками. Размер исходного полутонового изображения - 216 х 216 (время выделения контурных границ - 21 с). В данном случае диаметр входного участка оператора Хюккеля составлял 7 точек растра. Перекрытие при отслеживании контуров равнялось половине диаметра этого участка (а, следовательно, шаг между контурными точками - 3.5). Контуры приведенного изображения содержат 215 точек.

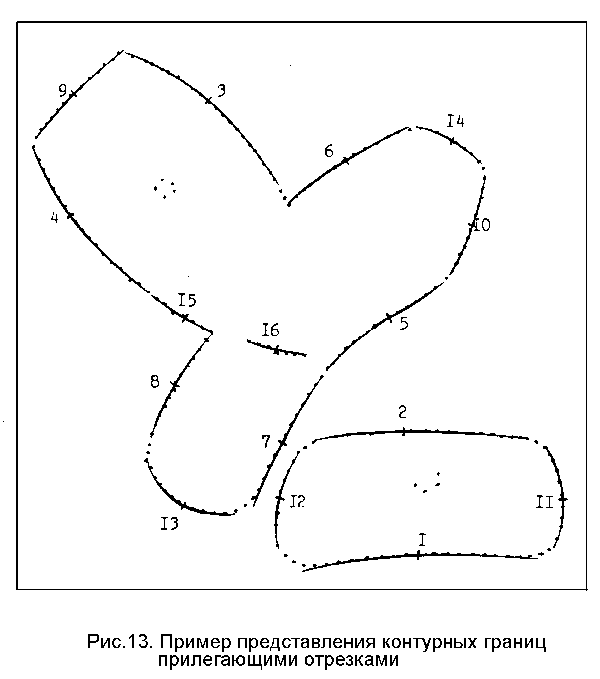
На этом же рисунке показаны результаты представления контуров прилегающими отрезками с помощью процедуры, при построении которой были учтены основные технические недостатки аналогичной процедуры, используемой на первом этапе.

Предложенная организация процедуры градиентного поиска, прореживание контурных точек и выбор начальных приближений, определяемых по наилучшим участкам контурных границ, позволили существенно сократить счетное время, необходимое для описания этих границ в терминах прилегающих отрезков на ЭВМ. Представление контурной картины, показанной на рис.13, прилегающими отрезками потребовало 50 с счетного времени ЭВМ БЭСМ-6, а картины того же порядка сложности, показанной на рис.10 (первая серия экспериментов [2]), с помощью первоначального варианта этой процедуры - свыше 20 мин.
 

Вернуться
 

Продолжение.