3.3. Применение метода накопления гипотез при распознавании объектов произвольной (криволинейной) формы

Перспективность использования методики накопления гипотез по сравнению с методикой непосредственной проверки подтвержденности гипотез, которую в данном случае можно назвать проверкой на совпадение с моделями-эталонами, зависит от конкретных особенностей решаемой задачи.

Методика непосредственной проверки на совпадение с моделями эффективна, когда требуется перебор небольшого количества гипотез, например, когда имеется возможность эффективного выделения высокоинформативных фрагментов, существенно ограничивающих множество порождаемых гипотез, либо когда характер задачи позволяет применить какую-либо стратегию, сокращающую перебор. В частности, это относится к случаю, когда мера сходства на допустимом множестве гипотез является гладкой функцией, имеющей ограниченное число экстремумов. В этом случае для поиска ее максимумов можно использовать градиентные процедуры. Такая стратегия поиска, например, применяется в предлагаемом способе представления контурных границ в терминах прилегающих отрезков.

В тех же случаях, когда по существу задачи имеются только малоинформативные первичные признаки (факты), каждый из которых в отдельности слабо ограничивает количество допустимых гипотез, преимущества методики накопления гипотез могут оказаться решающими, так как взамен многократного и, как правило, трудоемкого вычисления функции сходства здесь регистрируется простое совпадение точек в собственном пространстве гипотез.

Как и при поиске, в основе которого лежит вычисление функции сходства (поиска по принципу непосредственной проверки гипотез), выбор первичных признаков является ключевым, определяющим границы применимости методики накопления гипотез. Если использовать наиболее универсальные первичные признаки - контурные точки [20 - 22], то вычислительные ресурсы современных ЭВМ позволяют практически решать только задачу обнаружения двухпараметрических объектов (в частности, бесконечных прямых линий).

Для того чтобы ограничить число порождаемых гипотез до приемлемого уровня, при решении более сложных задач обнаружения (с большим числом неизвестных параметров) приходится использовать и более сложные первичные признаки (фрагменты) искомых объектов. Принципиальное затруднение при этом состоит в том, что следующие по сложности, наиболее естественные первичные признаки (прямолинейные контурные отрезки, соединяющие точки перегиба) резко ограничивают класс распознаваемых объектов. Как уже отмечалось, контурные границы объектов, имеющих плавные обводы (рис.20а), невозможно однозначно разбить на отдельные отрезки. Аппроксимирующие отрезки на таких контурах в общем случае невозможно зафиксировать достаточно четко. При этом, каждый отрезок порождает весьма обширное - "скользящее" - множество возможных положений искомого объекта. Именно здесь как нельзя кстати оказывается распознавание по принципу "накопления гипотез"...

Основная трудность при реализации такого алгоритма распознавания заключается в необходимости устойчивого определения ориентации и поперечного положения "скользящих" аппроксимирующих отрезков в случае реальных кривых, задаваемых дискретно и подверженных влиянию различных помех.

Если определять эти направления по коротким отрезкам (для того чтобы обеспечить общую универсальность алгоритма, независимо от формы объектов), то в реальных условиях случайные колебания этих отрезков будут приводить к весьма существенным колебаниям базисного вектора относительно его истинного положения. Например, если использовать элементы контура получаемые непосредственно с помощью оператора Хюккеля [5, 6] (как это предлагалось в [23]), то при диаметре входного участка в 7 точек растра, колебания концов получаемых элементарных контуров в "+-1 точку" приводят к колебаниям базисного вектора на расстоянии в 50 точек (что соответствует среднему расстоянию до центра фигуры "диаметром" в 100 точек) в пределах +-50/(7/2) - +-15 точек растра.

В этом случае приходится надеяться только на то, что искомое правильное решение все же получится за счет статистического усреднения. Такое решение предполагает организацию учета большого количества гипограмм, порождаемых отдельными элементарными отрезками, и, следовательно, требует значительных затрат машинной памяти для хранения накопителя гипотез, а также значительных затрат машинного времени на процедуру накопления гипотез и анализ полученной (в накопителе) картины.

С другой стороны, предложенное в [25] скользящее сопоставление по протяженным участкам контурных линий в принципе может удовлетворить требования по устойчивости, однако не обеспечивает универсальность, так как ограничивается только случаем прямолинейных отрезков (хотя и для этого случая здесь следует ожидать существенных затруднений по причине отсутствия эффективного способа аппроксимации отрезков).

В предложенной схеме реализации процедуры накопления гипотез используются скользящие отрезки, одновременно удовлетворяющие требованиям универсальности и устойчивости, а именно - прилегающие отрезки. Достоинства этих отрезков определяются тем, что, заложенное в их основу использование колоколообразной функции принадлежности контурных точек отдельному отрезку, позволяет эффективно отстраиваться от помех и, в целом, корректно - "по максимуму"- опираться на длину сопоставляемых контуров.

В результате удалось построить помехоустойчивую, конструктивно реализуемую процедуру распознавания объектов произвольной формы.

3.4. Особенности реализации процедуры распознавания плоских объектов произвольной формы

В рассматриваемой реализации предлагаемого метода распознавания поиск точки сгущения гипограмм ("порождаемых множеств"), отвечающих прилегающим отрезкам, выделенным на анализируемом изображении, осуществляется на основе представления пространства параметров как совокупности прямоугольных зон. При этом учет очередной гипограммы сводится к пометке зон, через которые эта гипограмма проходит, а задача поиска пересечения - к поиску зоны, помеченной наибольшим числом гипограмм. В программе, реализующей алгоритм, хранится информация только о помеченных зонах. Для этого отводится некоторый массив, в который запись делается с помощью хеширования (подробнее об этом сказано в Приложении 5).

Эталонные гипограммы ("порождаемые множества") строятся по отдельным полным неискаженным изображениям искомых объектов. В качестве точки приложения базисного вектора выбираются центры тяжести контурных границ, выделенных на этих изображениях. В процессе построения эталонных гипограмм шаг продвижения формального прилегающего отрезка непрерывно подстраивается с помощью обратной связи так, чтобы удержать соседние точки эталонной гипограммы в пределах одной зоны, на которые предполагается разбивать пространство искомых параметров.

Размер зон пространства искомых параметров по оси, определяющей наклон базисного вектора, выбирается согласно условию приблизительной эквивалентности сдвига и поворота эталонной фигуры: deltaA=deltaL/R, где deltaL - размер зоны по осям, определяющим положение точки приложения, а R - радиус объекта, т.е. среднеарифметическое длин радиусов-векторов, проведенных из центра тяжести к каждой из точек контурной границы.

При работе с дискретным представлением пространства искомых параметров возникает вопрос: что делать, если точка сгущения гипограмм попадает на стык зон? Так как гипограммы задаются поточечно с шагом, соизмеримым с линейными размерами зон, то в этом случае гипограммы могут пометить зоны таким образом, что исключается появление зоны с весом, равным количеству пересекающихся гипограмм. В результате тех же причин могут появиться случайные (ложные) точки сгущения (зоны, "вес" которых превосходит веса соседних). Для устранения подобных случайностей дискретной пометки в пределах соседних зон в программе, реализующей алгоритм, производится "сглаживание" полученной картины. Для каждой помеченной зоны вычисляется значение арифметической суммы содержимого соседних зон. Содержимое зоны - это число пометивших ее гипограмм. Соседними считаются 3х3х3 = 27 зон, включая центральную. Центр наиболее весомой зоны после выполнения процедуры сглаживания принимается в качестве искомой точки сгущения.

В [3] была предложена операция многократного сглаживания. В этом случае сглаживание выполняется итеративно до тех пор, пока не будет выполнено условие, что на двух последовательных этапах одна и та же зона (притом единственная) имеет максимальную сумму (среди всех зон на данном этапе). Центр этой зоны принимается в качестве искомой точки сгущения. Хотя такая процедура не продемонстрировала решающих преимуществ по сравнению с однократным сглаживанием, представляется целесообразным иметь ее в наборе средств анализа картины пересечения гипограмм. Многократное сглаживание согласует точку (зону) сгущения с ее окружением. Если эта точка находится на краю сгущения, то постепенно она сдвигается в его центр. Устойчивость этой точки (зоны) на нескольких последовательных этапах сглаживания является некоторой характеристикой ее общей надежности. Кроме того, если вершина сгущения не острая, т.е. в нее входит несколько зон, то за счет учета окрестных зон выделится одна зона максимального веса, положение которой будет зависеть от контекста (т.е. "весомости" окружающих зон).

3.5. Результаты экспериментов

Основные вопросы, на которые должны были ответить эксперименты, состояли в следующем: можно ли по прилегающим отрезкам, отвечающим различным участкам реальных кривых, определять положение искомого объекта с необходимой точностью, - будут ли гипограммы, порождаемые отрезками (прилегающими к контуру искомого объекта), проходить через точку пространства параметров, отвечающую истинному положению объекта? Кроме того, при экспериментальном моделировании нужно было также оценить возможность практической реализации предлагаемой схемы распознавания с учетом возможностей вычислительной техники.

Предлагаемый алгоритм был программно реализован на языке ФОРТРАН-ДУБНА (небольшая часть - на автокоде МАДЛЕН). Эксперименты с этой программой проводились на ЭВМ БЭСМ-6. Напомним, что производительность этой ЭВМ - 1 млн. опер./с, оперативная память - 32К слов по 48 разрядов.

Эталонные гипограммы распознаваемых предметов: стельки, далее называемой объектом N~1, утюга - N~2, футляра от очков - N~3 (см.рис.13), строились по их отдельным изображениям. Размер зон пространства искомых параметров составлял по осям, определяющим положение точки приложения, deltaL = 8 точек растра, по оси, определяющей наклон базисного вектора, deltaA = 0.1 рад. Линейный размер зон выбирался приблизительно равным минимальному расстоянию на котором "различимы" два параллельных контура. В данном случае это расстояние - "разрешение" - определялось диаметром входного участка оператора Хюккеля, с помощью которого выделялись элементы контурных границ. В данном случае этот диаметр составлял 7 точек растра (см. раздел 2.2). Конкретное значение "8" было выбрано как ближайшая "степень двойки", что существенно ускоряет операцию определения номера зоны (вместо деления - сдвиг...). Размер зон по углу выбирался согласно выше указанному критерию эквивалентности сдвига и поворота для фигур со средним радиусом в 50 точек растра (средний радиус объектов в данном случае).

При таких размерах зон эталонные гипограммы искомых объектов содержали соответственно 85, 60 и 45 точек.

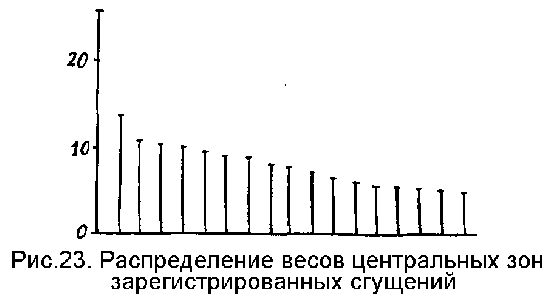
В процессе накопления гипотез о положении первого объекта на рис.13 было помечено 1784 зоны. Из них: четырехкратно - 1, трехкратно - 3, двухкратно - 47, однократно - 1733 (время накопления гипотез 1,5 с). Среди этих зон после операции сглаживания было зарегистрировано 18 сгущений (время сглаживания 1,0 с). Отдельные сгущения регистрировались по их центральным зонам. Центральная зона сгущения - это зона, вес которой превосходит вес любой зоны из ее ближайшего (3х3х3) окружения. На рис.23 показано распределение весов этих зон.

На рис.24 представлены гистограммы зон максимального веса наиболее мощных сгущений (здесь мощность сгущения определяется весом его центральной зоны).

Каждая гистограмма показывает значения наиболее весомых зон, находящихся на различных расстояниях от центральной зоны. Расстояния откладываются по горизонтальным осям и измеряются в единицах шага дискретизации. На гистограммах приводятся номера гипограмм, впервые появляющихся на данном расстоянии (нумерация отрезков на рис.25).

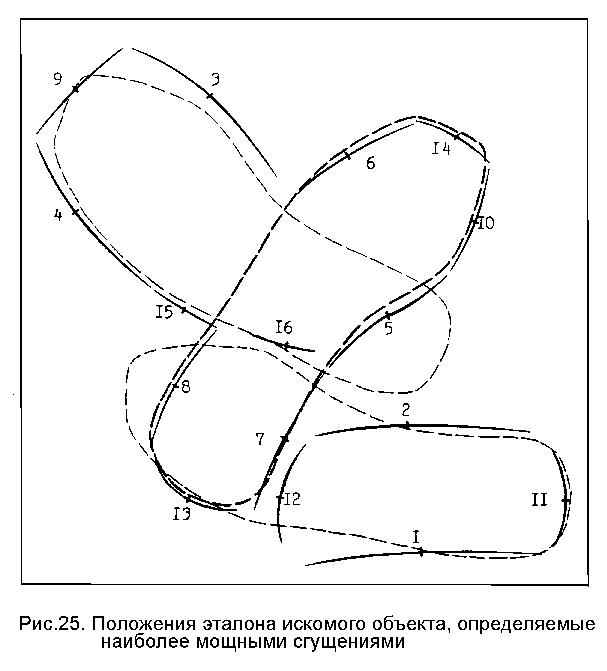
На рис.25 жирными штрихами показано положение эталона искомого объекта, определяемое центральной зоной (центральной точкой этой зоны) наиболее мощного сгущения (рис.24а). На этом же рисунке тонкими штрихами показаны положения эталона, определяемые двумя наиболее мощными "ложными" сгущениями (см. рис.24б,в).

Рис.26 иллюстрирует рациональность операции сглаживания.

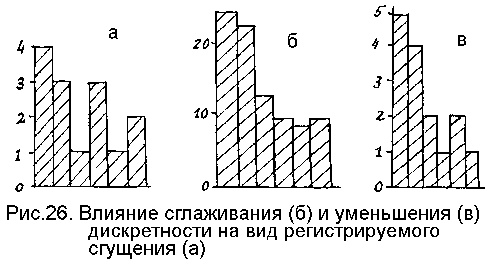
На рис.26а показана начальная гистограмма наиболее мощного сгущения (рис.24а и рис.26б). Здесь вес зоны - это число пометивших ее гипограмм. Рациональность операции сглаживания в данном случае подтверждается видом начальной гистограммы того же сгущения при размере зон, уменьшенном в полтора раза (рис. 26в). При этом соответственно несколько сдвинулись и центры зон пространства искомых параметров. Этот пример показывает, что относительно большой вес "побочного" выброса (рис.26а) обусловлен, в первую очередь, случайностями распределения точек гипограмм в пределах соседних зон.

Подобные эксперименты проводились с различными вариантами расположения прилегающих отрезков на контурных границах искомых объектов. В этой связи следует сказать, что при попытках зафиксировать прилегающие отрезки на представляемых контурах [3] получались самые различные расположения этих отрезков. В частности, для объекта N~1 (стельки) было проанализировано около десяти вариантов, которые включают приблизительно 70 (7 отрезков х 10 вариантов) различных положений для отдельного прилегающего отрезка (в том числе и самые неудачные, отвечающие участкам значительной кривизны). Во всех этих случаях точка пространства параметров, отвечающая истинному положению искомого объекта на текущем изображении, находилась в центральной зоне наиболее мощного сгущения. При этом все гипограммы, порождаемые отрезками, прилегающими к контуру искомого объекта, попадали (какими-либо своими точками) если не в эту зону, то в крайнем случае в одну из соседних.

В целом можно сделать вывод, что проведенные эксперименты подтвердили принципиальную работоспособность рассматриваемой схемы распознавания объектов произвольной формы и показали возможность ее конструктивной реализации.

3.6. Возможные усовершенствования

Следует отметить, что программная реализация предлагаемой схемы распознавания прежде всего предназначалась для проверки ее принципиальной работоспособности. Организацию работы программы можно значительно улучшить.

Принятая концепция эквивалентности прилегающих отрезков рассчитана на наихудшую ситуацию - случай очень гладких контуров, со слабо выраженными изменениями кривизны. Естественно, в общем случае при сопоставлении прилегающих отрезков следует учитывать, хотя бы грубо, параметры их ветвей. Со всей очевидностью это показывают приведенные примеры ложных положений искомого объекта (см. рис.25). Если пятка стельки приблизительно вписывается в прилегающие отрезки, представляющие контур футляра от очков, а ее носок - в контур утюга, то подтверждение прямолинейного участка контурной границы искомого объекта криволинейным отрезком N~13, а криволинейного участка - прямолинейным отрезком N~2, только на основе их взаимного касания явно не оправдано. Организация иерархического учета гипограмм, т.е. накопления гипотез в порядке их вероятности, - задача дальнейших исследований. Причем этот вопрос имеет принципиальное значение, так как при этом должен значительно уменьшиться относительный вес ложных точек сгущения.

Весьма перспективным представляется также исследование вопроса использования конфигураций начального сопоставления (первичных фрагментов), построенных из нескольких (прежде всего из пар) соседних прилегающих отрезков.

Для сокращения требуемой вычислительной мощности поиск по принципу накопления гипотез можно выполнять итеративно: вначале работать с большими зонами и грубым представлением гипограмм, а затем анализировать зоны пересечения, используя более точное представление и более мелкие зоны.

Другой способ надежной регистрации пересечения гипограмм (без использования сгаживания) заключается в пометке всех вершин каждой зоны. При увеличении размерности пространства искомых параметров затраты на дополнительную память могут оказаться меньшими, чем на вычисление локальных (окрестных) сумм. В связи с этим целесообразно было бы решить задачу разбиения пространства параметров на зоны, имеющие минимальное число вершин (для двухпараметрического пространства - это треугольники, для трехпараметрического - тетраэдры и т.д.).

Естественно, реализация предлагаемой схемы может оказаться слишком громоздкой для прямого распознавания сложных объектов, - объектов, контурные границы которых требуют для своего описания порядка десяти и более прилегающих отрезков. Здесь предлагаемая схема может быть применена для распознавания отдельных фрагментов таких объектов, используемых в дальнейшем для окончательного решения задачи распознавания с помощью структурных методов либо последующего непосредственного сопоставления моделей (эталонов) искомых объектов с анализируемыми картинами. В целом именно в выделении таких фрагментов, уже достаточно четко соответствующих отдельным частям реальных объектов, можно видеть основное предназначение предлагаемой схемы распознавания.

Возможно, что учет более тонких характеристик прилегающих отрезков, а также усовершенствования техники реализации предлагаемой схемы распознавания позволят распространить ее на распознавание объемных тел по их изображениям, во всяком случае - их фрагментов. При этом для ограничения объема гипограмм существенно помогло бы использование прилегающих ("скользящих") поверхностей, описывающих дальностную картину. Это описание может быть получено в результате анализа полутоновых изображений, методами стереозрения либо прямым дальнометрированием (например, с использованием лазерной техники).

З А К Л Ю Ч Е Н И Е

Перечислим основные концепции, положенные в основу построения предлагаемой схемы распознавания объектов произвольной формы.

1. Отдельный отрезок простейшей формы (плавный отрезок, не содержащий явных перегибов) четко фиксирует проходящий контур только в направлении собственной нормали. Четко расположить контурную фигуру можно только по сочетанию таких скользящих отрезков.

Аппроксимация контурных границ отрезками более сложной формы, которая могла бы привести к более жесткому ограничению возможных положений объекта, возвращает нас к задаче предварительного выделения простейших отрезков, и, по существу, эквивалентна задаче выделения объекта в целом.

2. Методика накопления гипотез открывает принципиально новые "технические" возможности конструктивного решения задачи целостного распознавания контурных объектов в условиях скользящего ("нечеткого") первичного сопоставления контуров.

Конечная ориентация на методику непосредственной проверки гипотез о положении и ориентации искомых объектов, т.е. на методику сравнения с эталонами (как, например, в [32, 33] и др.), для сокращения количества проверяемых гипотез вынуждает обращаться к задаче выделения достаточно характерных начальных фрагментов искомых объектов. Последняя же задача, а именно - задача поиска контурных отрезков нетривиальной ("не простой" - "составной") формы в принципе не проще задачи выделения объекта в целом.

Потенциальную возможность конструктивного выхода из этого "замкнутого круга" и дает скользящее начальное сопоставление с последующим решением задачи распознавания по принципу накопления гипотез.

3. Разработка концепции прилегающих отрезков позволяет реализовать эту возможность, - образно говоря, эта разработка "дотягивает" уровень определенности первичных отрезков (по части четкости определения поперечного положения и ориентации) до "максимиально возможного" (когда задача выделения первичных отрезков еще принципиально более проста. чем выделение целой фигуры), - до того уровня, с которого уже задачу целостного распознавания может конструктивно "подхватить" методика накопления гипотез.

С этих позиций предлагаемая схема распознавания объектов произвольной формы представляется одной из наиболее перспективных схем автоматического решения этой задачи.

Естественно, необходимо отдавать себе отчет, что эта схема имеет существенное ограничение, - она применима только к объектам хотя и произвольной, но в принципе известной - фиксированной - формы. Эта схема предназначена для работы в реальных условиях, - когда задача распознавания может быть решена только за счет жестких ограничений на модели искомых объектов. Задача распознавания объектов "нежесткой" формы - это в принципе "другая" задача, - задача, которая решается в условиях достаточно полной исходной информации, и, более того, в условиях возможности ее последовательного целенаправленного уточнения. Тем не менее, и здесь предлагаемая схема распознавания объектов могла бы иметь место. Возможно, что допустимым изменениям формы искомого объекта будут отвечать закономерные изменения формы сгущения порождаемых гипограмм, - подобные, например, изменениям формы светового пятна при покачивании фокусирующей линзы (такие исследования были бы весьма полезны для "сознательного" учета геометрических искажений вносимых оптикой, - для их возможно более четкого отличия от случаев принципиально "не тех" объектов).
 

Вернуться
 

Продолжение.