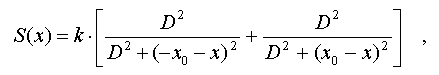
Where k - number
of points in each segment.
Extrema of such
measure are determined by zero values of its derivative:
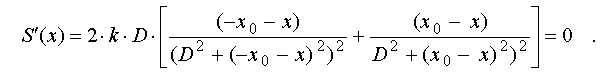
The denominator
of resulting expression is positive at any values of entering variables.
The numerator can be transformed to the view
![]()
This equation
has five solutions, one of which is x_1 = 0, and four others :
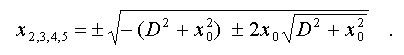
Two solutions
which are determined by a difference of the expressions placed under
sign of exterior square root, have imaginary values at any values of
entering variables (as x_0> 0, under the initial agreement - see fig.5a).
Others two have real values, when
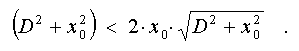
Simplifying
this expression, we shall obtain that at D < sqrt(3)*x_0 investigated
conformity function has three extremums: one central and two symmetric side
ones. It is easy to show, that:
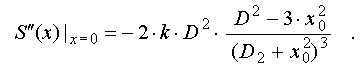
It is obvious,
if D < sqrt(3)*x_0, then S"(x)|_0 > 0, i.e. the central extremum
is a local minimum of considered conformity function of and, hence,
adjacent side exremums are local maximums of this function (see fig.5b).
At D > sqrt(3)*x_0, these maximums merge in one (see fig.5c). Positions
of maximums depending on a value of parameter D are shown on fig.5d
(see the formula for an evaluation of x_2... x_5).