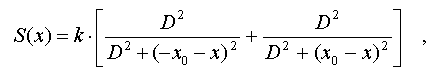
где k - число точек в каждом
отрезке.
Экстремумы такой меры определяются
нулевыми значениями ее производной:
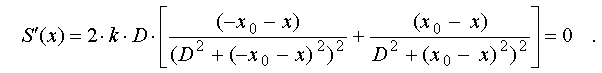
Знаменатель результирующего
выражения положителен при любых значениях входящих переменных. Числитель
можно преобразовать к виду
![]()
Это уравнение имеет пять
решений, одно из которых x_1 = 0, и четыре других:
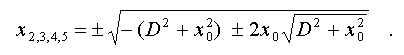
Два решения, которые определяются
разностью выражений, стоящих под знаком внешнего квадратного корня,
имеют мнимые значения при любых значениях входящих переменных (так как
x_0 > 0, по начальному соглашению - см. рис.5a). Два других имеют
действительные значения, когда
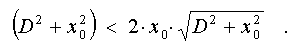
Упрощая это выражение, получим,
что при D < sqrt3*x_0 исследуемая функция сходства имеет три экстремума:
один центральный и два симметричных боковых. Нетрудно показать, что:
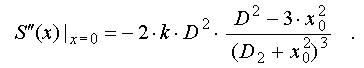
Очевидно, если D < sqrt(3)*x_0,
то S"(x)|_0 > 0, т.е. центральный экстремум является локальным минимумом
рассматриваемой функции сходства и, следовательно, соседние боковые
- локальными максимумами этой функции (см. рис.5b). При D > sqrt(3)*x_0,
эти максимумы сливаются в один (см. рис.5c). Положения максимумов в зависимости
от значения параметра D показаны на рис.5d (см. формулу для вычисления
x_2...x_5).