| English |
1.7.A. К вопросу
автоматической коррекции ширины функции принадлежности.
Как утверждается, максимум
функции сходства, определяемого выражением
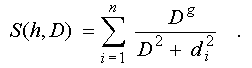
достигается при конечной величине
параметра D, когда показатель степени, в которую он возводится в числителе
- g (регулирующий скорость роста амплитуды) лежит в интервале 1 < g <
2.
Докажем это утверждение.
Будем рассматривать аппроксимируемый
отрезок (см. рис.6b) как непрерывное множество точек. В этом случае мера
сходства определяется интегралом
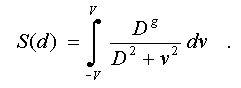
Здесь переменная v = d введена
для того, чтобы избежать путаницы с обозначением дифференциала. Поведение
этой меры в зависимости от ширины функции принадлежности определяется производной
по D:
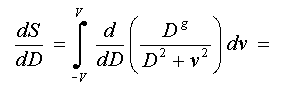
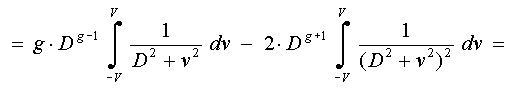
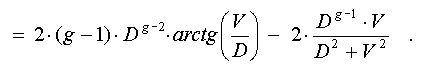
Приравнивая это выражение
нулю, и вводя переменную gamma = V/D, получаем:
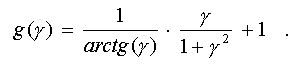
В интересующем нас диапазоне
(0 < gamma < oo) эта функция имеет максимальное значение 2 при gamma=
0 и асимптотически приближается к 1 при gamma -> oo (см. рис.6d).
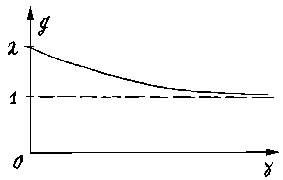
|
| Рис.6d |
Монотонность ее убывания
подтверждается тем, что ее производная всюду отрицательна на интервале
0 < gamma < oo:
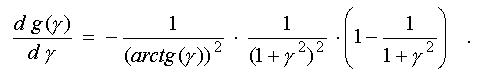
График, собственно интересующей
нас, обратной функции D/V=1/gamma(g), представлен на рис.6c. Этот график
показывает, какой будет ширина функции принадлежности (по сравнению с текущей
относительной шириной аппроксимируемого отрезка) при достижении рассматриваемой
мерой сходства своего максимального значения в зависимости от показателя
g, регулирующего скорость роста амплитуды функции принадлежности.