1.2. Бел-аппроксимация в задаче описания контурных границ

Прежде всего следует отметить, что поиск минимума среднеквадратичного отклонения представляет собой принципиально более простую задачу, чем поиск локальных максимумов нечеткой меры сходства, - что определяется "простотой" параболы по сравнению с "колокольчиком". В частности, для случая среднеквадратичной аппроксимации прямыми линиями существует аналитическое решение. Еще один пример аналитического решения задачи нахождения минимума среднеквадратичного отклонения - оператор Хюккеля [5, 6]. Кроме того, известно много случаев эффективной реализации процесса нахождения максимумов взаимной корреляции для различного вида образов (при этом, по существу, находится минимум среднеквадратичного отклонения [7]).

Поэтому в целом естественно стремление остаться, по возможности, в рамках "чистого" среднеквадратичного отклонения.

Однако, как было показано, величина среднеквадратичного отклонения по своей сути отражает глобально-усредненное сходство модели (т.е. примеряемого образа) с анализируемым образом. В этом случае мера сходства монотонно убывает с увеличением отклонения любого элемента анализируемого образа от соответствующего элемента примеряемой модели.

Получение адекватного описания какой-либо картины с помощью такой меры сходства возможно только в случае, когда среди сопоставляемых моделей присутствует модель всего анализируемого образа. В этом случае, минимизируя суммарное отклонение, мы можем получить искомый результат, т.е. найти соответствующую модель. Иначе мы получим "усреднение" анализируемого образа одной из имеющихся моделей, что может не иметь ничего общего с необходимым результатом - адекватным описанием данного образа или хотя бы его части.

Эффективность использования критерия суммарного (среднеквадратичного) отклонения непосредственно зависит от того, насколько четко мы можем выделить аппроксимируемый образ из его окружения, либо насколько полно мы можем отразить анализируемую картину какой-либо целостной моделью. С этой точки зрения можно выделить два подхода в решении задачи описания картин различного вида на основе минимизации среднеквадратичного отклонения:

- аппорксимация исходных данных целостными моделями (см., например, [8 - 12]), в частности, контурные границы - цепочками отрезков;

- пследовательное независимое выделение и аппроксимация отдельных образов, входящих в состав анализируемой картины [1, 5, 6, 13], в частности, отдельных отрезков контурных границ.

Адекватность анализируемым картинам представлений, получаемых на основе первого подхода, обеспечивается в первую очередь тем, что здесь элементы (точки) исходных данных в итоге будут распределены между соответствующими элементами (отрезками) примеряемых моделей и не будут оказывать столь негативного "оттягивающего" влияния на смежные элементы (отрезки) примеряемой модели. Например, если аппроксимировать угол (см. рис.1, 3) соответствующей целостной моделью (цепочкой из двух отрезков), то, в принципе, можно получить адекватный результат даже в рамках "чистой" среднеквадратичной аппроксимации.

Однако такой подход эффективен только как "подстроечный", когда априори имеется первичное приближение - модель уже достаточно хорошо отражающая анализируемую картину, - модель, которую остается только "подстроить". Прерогатива определения таких "первичных" моделей остается за вторым подходом - последовательным контекстно-независимым выделением и аппроксимацией отдельных подобразов.

В решении этой задачи, в свою очередь, также можно выделить два подхода, в зависимости от способа выделения элементов принадлежащих отдельным подобразам:

- выделение "неуправляемое" примеряемыми моделями в процессе аппроксимации [5, 6, 13];

- выделение "управляемое" в процессе аппроксимации (см., например, [1]), - отбрасывание элементов, находящихся вдали от соотвествующих элементов примеряемой модели.

Достоинством первого подхода заключается в том, что при его применении средеквадратичное приближение используется в своем "чистом" виде, с вытекающей осюда вычислительной простотой. Однако, такой подход применим только для представления анализируемых картин простейшими - элементарными образами, в терминах которых, в принципе, может быть достаточно адекватно представлен любой произвольно выбранный участок описываемой картины (во всяком случае, - большинство таких участков). Такое требование может быть выполнено только для представления в терминах простейших образов, находящихся "на уровне" дискретности задания исходных данных. Для изображений такими элементами являются участки размером в несколько точек растра (порядка 5 - 10). Только на таких участках, контурные границы с достаточной точностью могут быть представлены прямолинейными отрезками - простейшими универсальными образами, в терминах которых в принципе может быть описана произвольная контурная конфигурация.

Достоинством второго подхода является возможность работы с протяженными образами, дающими более "осмысленное" описание анализируемых картин. Однако в этом случае существенно усложняется "техника" решения задачи аппроксимации. Задача становится многоэкстремальной, требующей в принципе для своего решения использования начальных приближений, получаемых вне этого подхода. Кроме того, обычное использование при этом пороговой функции принадлежности приводит к неустойчивости процесса аппроксимации...

И если задача выбора начальных приближений в принципе решается на основе первого подхода, - выделения простейших образов, то проблема "некорректности" порогового отбрасывания "посторонних" точек до сих пор практически не решалась.

Именно здесь играет свою решающую роль колоколообразная (нечеткая) функция принадлежности. Замена пороговой функции на колоколообразную, при построении меры сходства аппроксимирующих моделей (отрезков) и описываемых данных (контурных границ), позволяет ослабить критичность при определении принадлежности элементов исходных данных к отдельному аппроксимируемому образу. Колоколообразная функция принадлежности сглаживает разрывы функции сходства, обусловленные дискретностью представления контурных границ, а также случайными помехами, что позволяет применять простые градиентные процедуры при поиске ее экстремумов. Кроме того, расширение "оснований" искомых максимумов (обусловленное ветвями колоколообразной функции принадлежности) обеспечивает меньшую критичность в выборе начальных приближений. Эксперименты (в том числе и на реальных изображениях) подтвердили справедливость этих положений (см. раздел 2.1).

В целом, анализ особенностей различных подходов в решении задачи аппроксимации контурных границ приводит к выводу о целесообразности их комплексного, последовательного использования. В начале, с помощью процедур "чистой" среднеквадратичной аппроксимации контурное изображение можно описать в терминах простейших линейных элементов. Затем, наилучшие из них (определяемые минимальными значениями величины отклонения) - использовать в качестве начальных приближений для последующей процедуры максимизации нечеткой меры сходства, получая в результате описание протяженными отрезками; после чего в случае необходимости можно подстраивать параметры этих отрезков как целостной совокупности, перераспределяя контурные точки между ними.

В заключение этого раздела следует остановиться на общих методологических достоинствах концепции колоколообразной - нечеткой - функции принадлежности. В принципе, в задаче описания реальных контуров, возможно применение вероятностных оценок принадлежности контурных точек к отдельному образу [14, 15, 16]. Однако, как показывают эксперименты, лежащая в основе этого подхода статистическая модель контурных границ, в которой сигналы представляют прямоугольные перепады (идеальные отрезки), искаженные нормальным шумом, является теоретической идеализацией, весьма далекой от действительности. Реальные искажения контурных границ - это различные искривления, пятна, вырывы и т.п., учет которых в теоретико-статистических моделях вызывает существенные затруднения, и отвлекают от сути решаемой задачи (которая в данном случае заключается в "выведении" аппроксимирующего отрезка на осевую линию представляемого участка контурных границ, с корректным ограничением влияния посторонних точек).

Более плодотворным представляется решение задачи описания контурных границ в терминах отрезков осевых линий как задачи поиска максимумов нечеткого сходства с постулированием нечеткой - колоколообразной функции принадлежности, а не посредством конструирования строгих моделей исследуемых сигналов. При этом относительно этих сигналов предполагаются только самые общие свойства, а именно - значительная "разреженность" множества отрезков линий, каждый из которых может быть искажен отдельными выбросами, искривлениями и т.п.

Сказанное выше можно дополнить утверждением, высказанным в работе [17]: "...убеждение многих исследователей в том, что теория статистических решений дает какую-либо более строгую и объективную классификацию, чем другие алгоритмы принятия решений, является формалистическим заблуждением...объективной меры (близости) нет в силу субъективного характера постановки задачи распознавания образов...более важным, по-видимому является, вопрос о простоте определения меры близости (сходства) ...". Для многих задач вполне достаточно использования концепций нечеткой (колоколообразной) функции принадлежности и нечеткой меры сходства, как, например, в рассматриваемом способе аппроксимации контурных границ. При этом существенно упрощаются построение и модификация процедур распознавания - аппроксимации, например, совершенно естественно вводятся необходимые по ходу решаемой задачи изменение ширины функции принадлежности и нечеткость (размытость) концов аппроксимирующих отрезков (см. последующие разделы).

1.3. Выбор и автоматическая коррекция ширины функции принадлежности

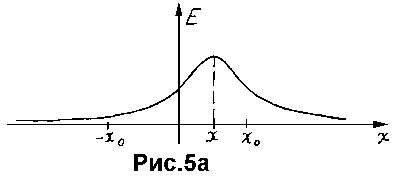
Получение каких-либо строгих аналитических оценок, характеризующих эти явления в общем случае, представляется весьма сложной задачей. Решающую роль здесь, очевидно, должны играть экспериментальные исследования. В качестве приблизительных оценок можно использовать результаты анализа простейшего случая, а именно случая двух параллельных отрезков. На рис.5а показано поперечное сечение данной картины. Положение отрезков здесь определяется точками x0 и -x0, а положение осевой линии аппроксимирующего отрезка определяется параметром x.

Аналитические исследования, проведенные на базе предложенного выражения функции принадлежности, показали, что функция сходства в этом случае имеет отдельные максимумы, отвечающие двум параллельным отрезкам, если ширина функции принадлежности имеет величину, меньшую, чем расстояние между этими отрезками, увеличенное в sqrt(3) раз (рис.5б).

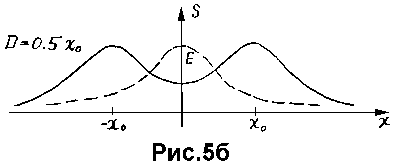
Если это не так, то максимумы сливаются в один (рис.5в). Доказательство этого утверждения приведено в Приложении 1.

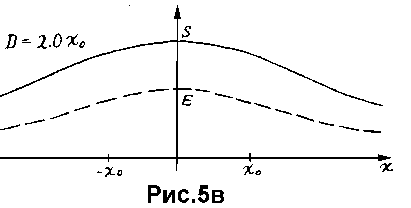
На рис.5г показаны положения максимумов в зависимости от значения параметра D. На этом рисунке, для того чтобы сохранить соответствие горизонтальной оси предыдущим рисункам, независимая переменная D откладывается по вертикальной оси. Погрешность оценки положения искомых отрезков по максимумам рассмотренной меры сходства резко уменьшается с уменьшением ширины функции принадлежности и, например, уже при D < x_0 не превышает 0.1 величины расстояния между отрезками, а при D < 0.5*x_0 - 0.01 той же величины.

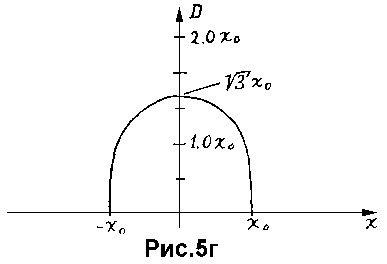
Приведенные результаты аналитических исследований позволяют оценить условия слияния соседних точек аппроксимируемых контуров. При ширине функции принадлежности, превышающей шаг дискретности представления исследуемых контурных отрезков более чем в sqrt(3) раз, функция сходства будет иметь один общий локальный максимум для каждых двух соседних точек, даже при перемещении аппроксимирующей линии перпендикулярно к отрезку, соединяющему эти точки.

В целом представляется естественной такая организация процесса поиска локальных максимумов нечеткой меры сходства, при которой ширина функции принадлежности изменяется в процессе поиска. Вначале можно задавать ее достаточно большой, обеспечивающей только разделимость отрезков, а затем уменьшать ее в соответствии с уменьшением рассогласования между осевой линией и представляемым контурным отрезком. Такая организация процесса должна обеспечить высокую точность оценки положения контурных отрезков и при этом уменьшить вероятность нахождения ложных максимумов. В этом случае начальную ширину можно выбирать весьма приблизительно, руководствуясь простейшими полученными оценками для разрешающей способности бел-аппроксимации.

Коррекцию функции принадлежности предлагается осуществлять путем непосредственного введения ее ширины в число искомых параметров меры сходства и использования такой функции принадлежности, у которой амплитуда при уменьшении ее ширины возрастает (рис.6а):

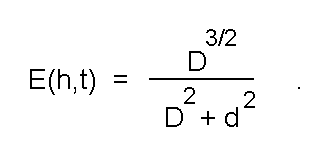
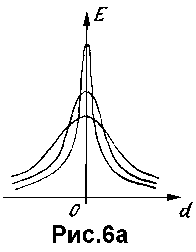
В итоге, выражение, определяющее меру сходства приобретает следующий вид:

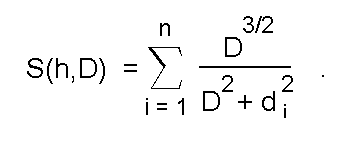
В этом случае при каждом фиксированном наклоне осевой линии локальный максимум такой меры достигается при D = 0.7*V, где V - относительная полуширина представляемого отрезка (половина длины его проекции на направление, перпендикулярное к текущему направлению осевой линии, рис.6б). В процессе поиска очередного максимума такого сходства с уменьшением рассогласования между представляемым отрезком и осевой линией будет соответственно уменьшаться и ширина функции принадлежности, обеспечивая тем самым необходимую точность определения положения отрезка.

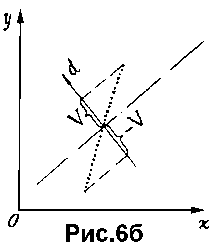
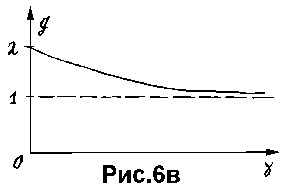
Чувствительность такой меры сходства к относительной ширине отрезка связана с тем, что теперь при увеличении ширины функции принадлежности одновременно с увеличением "вклада" удаленных точек в значение функции сходства уменьшается вклад точек, находящихся вблизи осевой линии. Причем равновесие между изменениями этих вкладов наступает при конечной величине параметра D, когда числитель в выражении для меры сходства D\g (регулирующий скорость роста амплитуды), имеет показатель степени, лежащий в интервале 1 < g < 2 (рис.6г).

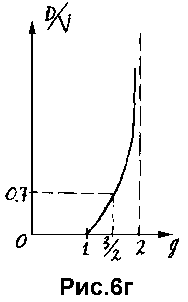
На этом рисунке приведен график значений отношения D/V, при которых мера сходства имеет максимальное значение в зависимости от параметра g (доказательство этого утверждения приведено в Приложении 2). В данной работе использовалось значение показателя степени g = 3/2, что упрощает вычисления и приводит к устойчивому слежению за относительной шириной отрезка . При этом, как уже отмечалось, D = 0.7*V.
 
 
 
 
 
 
 

Вернуться
 

Продолжение.