ПРИКЛАДНЫЕ ВОПРОСЫ ГЕОМЕТРИИ ЛИНИЙ.

КОЛОКОЛООБРАЗНАЯ (НЕЧЕТКАЯ) ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ В ЗАДАЧЕ СРУКТУРНОЙ СЕГМЕНТАЦИИ – АППРОКСИМАЦИИ КОНТУРНЫХ ОБЪЕКТОВ ПРОИЗВОЛЬНОЙ – КУСОЧНО-ГЛАДКОЙ ФОРМЫ.

УНИСОН ПОЗИЦИОННЫХ ГИПОТЕЗ КАК ИНДИКАТОР ОБНАРУЖЕНИЯ ЗАДАННЫХ КОНФИГУРАЦИЙ.

ШУЛЬГА В.И.

https://shulga.tripod.com/A_SAD2/R.htm
English

                  АННОТАЦИЯ

Наглядно демонстрируется физический смысл минимизации среднеквадратического отклонения, – классической основы аппроксимации реальных данных. Показывается необходимость использования колоколообразной функции принадлежности при решении задач аппроксимации (сегментации) в реальных условиях.
Предлагается новое геометрической понятие – отрезки с нечеткими концами. Такие отрезки декларируются в качестве максимально устойчивых (геометрически определенных - строгих) универсальных элементов первичного описания линейных образов произвольной – криволинейной формы.
Описывается процедура быстрого позиционного обнаружения, основанная на регистрации унисона параметрических (позиционных) гипотез. Предлагается смысловое обобщение подобных процедур, в том числе – восходящих к широко известным преобразованиям Хо. 
Решается задача позиционного обнаружения контурных объектов произвольной формы в тесном – частично перекрывающем контексте.

Ключевые слова:
моделирование данных, регрессионный анализ, интерполяция, аппроксимация, сегментация, кусочно-гладкие кривые, сплайны, нечеткие множества; анализ формы, анализ изображений, распознавание образов, распознавание изображений, сравнение с эталоном, преобразование Хо; компьютерное зрение, машинное зрение, индустриальное зрение, зрение роботов, распознавание чертежей, анализ документов, схем, карт, графиков, траекторий и сигналов в целом; прикладная геометрия.

ВВЕДЕНИЕ.
Концептуальное содержание.
В настоящей работе рассматривается вопрос помехоустойчивого представления контурных изображений в виде совокупности элементарных отрезков. Рассматривается вопрос последующего позиционного обнаружения (обнаружения с определением положения и ориентации) среди этих совокупностей заданных конфигураций. Искомые конфигурации задаются своими образцами (эталонами), которые, в данном исследовании, представляются одиночными контурными изображениями кусочно-гладких объектов. В качестве исходного материала использовались контурные препараты реальных полутоновых изображений.
Линия – одно из первичных геометрических понятий, с помощью которых человек описывает окружающую действительность. Кажущаяся легкость – «очевидность», с которой человек оперирует своими абстрактными представлениями в этой области, создает ложное впечатление о несложности алгоритмизации (переложения на компьютер) такого оперирования. Одна из ключевых задач здесь – разбиение регистрируемых линейных образов на отдельные составляющие – элементарные отрезки. Трудности начинаются уже в простейшем случае – случае «угловатых» – ломаных линий. Оказывается, весьма непросто зарегистрировать угол в реальности, когда линии задаются дискретно, как совокупность отдельных точек, разбросанных относительно своего истинного положения.

В первом разделе настоящей работы систематически разбираются возникающие здесь трудности. Рассматривается физический смысл мнимизации средне-квадратического отклонения - базовой процедуры анализа реальных данных. Наглядно демонстрируется необходимость использования колоколообразной (нечеткой) функции принадлежности контурных точек к отдельному отрезку. Задачи разбиения контурной конфигурации на отдельные отрезки и их аппроксимации сводятся воедино - к поиску локальных максимумов меры "нечеткого" сходства построенной на базе такой функции.

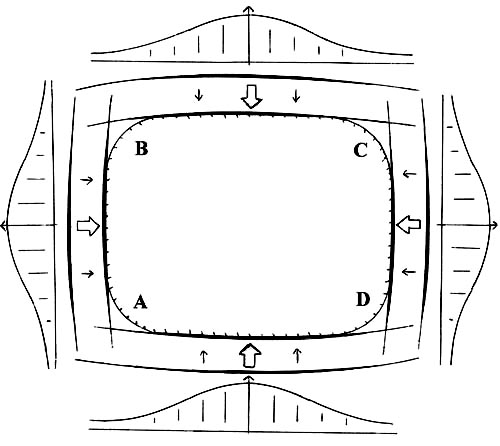
Во втором разделе рассматривается принципиально более сложная задача, а именно задача разбиения на примитивы линий, имеющих плавные очертания, – на которых вообще нет четких углов, когда один отрезок плавно переходит в другой. Пример фигуры, ограниченной подобной линией показан на рис.I.
FigI
Рис.I
В центральной части этого рисунка представлен четырехугольный овал – ABCD (ContourI ), который можно трактовать и как овальный четырехугольник (контур кухонной раковины, или – экрана кинескопа со скругленными углами ~ 35ЛК…). Четко зафиксировать моменты отхода - отрыва контура такой фигуры от приближающих линейных образов – аппроксимирующих отрезков в принципе невозможно. Ситуация усугубляется и тем, что не существует какого-либо ограниченного набора лекал, исчерпывающих все многообразие форм простейших – элементарных кривых, - кривых минимальной кривизны. В общем случае можно рассчитывать только на более-менее точное прилегание аппроксимирующих отрезков – лекал – по центру (середине), с постепенным расхождением к периферии.

Плавное расхождение – это принципиальный момент, который необходимо включить в модель приближающих образов. Функция, оценивающая принадлежность точек к отдельному отрезку должна иметь максимум по центру отрезка, и постепенно уменьшать свое значение на его периферии. Такая - колоколообразная функция позволяет в максимальной степени опираться на длину линейного образа при его аппроксимации кривыми какого-либо простейшего типа, - в наибольшей степени по центру, с постепенным ослаблением к периферии, в соответствии с их постепенным расхождением. На рис.I схематически показаны линейные образы, определяемые данной концепцией. Уменьшение их толщины (их утончение) отвечает уменьшению их геометрической определенности – четкости. Соответствующие образы колоколообразной функции принадлежности изображены с внешней стороны каждого отрезка. Наглядно можно представлять, что аппроксимация осуществляется некими дугами - дужками с утончающимися концами (уместна ассоциация и с типографскими круглыми скобками). Такие отрезки – дужки названы прилегающими отрезками, потому что их ветви, в общем, только прилегают к аппроксимируемым линиям. Их другое смысловое название – отрезками с нечеткими концами.

К понятию прилегающих отрезков – отрезков с нечеткими концами можно подойти и с другой стороны, - не со стороны уменьшения их четкости на периферии, а, наоборот, – ее увеличения к центру. Увеличение геометрической определенности к центру – середине, с прилеганием ветвей, - это как раз то, что обеспечивает максимум четкости в определении касательного направления. Здесь, абстрактная – дифференциальная характеристика – направление линии в точке (первая производная), приобретает в образе прилегающих отрезков устойчивое основание для своего определения в реальных условиях. Появляется потенциальная возможность более широкого практического использования этой характеристики при анализе реальных данных. 
Представляется весьма вероятным, что подобным образом прилегающие отрезки переводят из мира абстракций в реальность и дифференциальную характеристику второго порядка – кривизну. Хотя напрямую это и не исследовалось, тем не менее, общий характер - вид результатов экспериментальных исследований определенно демонстрировал, что и здесь прилегающие отрезки могут быть устойчивым основанием.
Во втором разделе рассматриваются общие принципы и технические особенности реализации концепции прилегающих отрезков. Приводится общий вид функции сходства, локальными максимумами которой определяются эти отрезки. Обсуждаются результаты экспериментальной проверки.

В третьем разделе рассматривается вопрос практического использования прилегающих отрезков в задаче позиционного обнаружения контурных объектов произвольной формы по их образцам. Предлагаемое решение базируется на методике регистрации унисона параметрических (позиционных) гипотез о возможных положениях искомой конфигурации, которые независимо порождаются отдельными первичными признаками – фрагментами. В качестве таких признаков – фрагментов здесь выступают прилегающие отрезки. Приводится (предлагается) общая онтологическая (сущностная) схема такой методики. Практическая реализация этого подхода приводит к процедуре обнаружения подобной процедурам, в основе которых лежит известное преобразование Хо. Предлагаемая трактовка позволяет увидеть их глубинную общность - упростить логику их разработки и дальнейшего развития.

Кроме того, и это самое главное, рассматриваемая разработка базируется на использовании элементов первичного сопоставления, дающих максимум геометрической определенности в случае объектов произвольной формы. Используются упомянутые выше прилегающие отрезки. Прилегающие отрезки решающим образом ограничивают множество порождаемых гипотез. Именно это позволило дотянуть позиционное обнаружение посредством регистрации унисона гипотез до возможности конструктивной реализации. С другой стороны, именно такой способ обнаружения позволил принципиальным образом вытянуть «скользящую неопределенность» прилегающих отрезков, имеющую место в общем случае. Можно говорить об уникальном единстве этой концептуальной пары.
На этой основе, была разработана помехоустойчивая последовательность процедур, решающая задачу сегментации – аппроксимации, а также целостного позиционного обнаружения (обнаружения с определением положения и ориентации) контурных фигур произвольной формы по их эталонам, когда искомый образ может частично перекрываться другими объектами.

Все это может иметь дальнейшее развитие и широкое применение, как по отдельности, так и в целом.

ОГЛАВЛЕНИЕ – СОДЕРЖАНИЕ.

1. БЕЛЛ-АППРОКСИМАЦИЯ.

2. ПРИЛЕГАЮЩИЕ ОТРЕЗКИ.

3. УНИСОН ПАРАМЕТРИЧЕСКИХ ГИПОТЕЗ КАК ИНДИКАТОР
ПОЗИЦИОННОГО ОБНАРУЖЕНИЯ.

ВЫВОДЫ.

СПИСОК ЛИТЕРАТУРЫ.
ПРИЛОЖЕНИЯ.

В своей основе, данная статья представляет собой иначе акцентированный, терминологически усовершенствованный вариант работы:
Шульга В.И. «Комплекс помехоустойчивых процедур аппроксимации контурных границ и распознавания объектов на контурных изображениях (исследовательская разработка)» / Институт кибернетики имени В.М.Глушкова АН Украины, Киев, 1992, 75стр. / Депонировано во Всесоюзном институте научной и технической информации (ВИНИТИ), Москва, 04.01.92, N 12-B92.
https://shulga.tripod.com/GEOLIN/glnfl1.htm
В свою очередь, эта работа обобщает исследования автора, первые публикации о которых датируются 1981-ым  [2] и 1982-ым [19] годами. В научной литературе имеется множество статей, тематика которых пересекается с тематикой настоящего исследования. В Интернете находится множество сайтов по запросам – «weighed least squares»-«взвешенный квадрат», «fuzzy lines»-«нечеткие линии», «generalized Hough transform»-«обобщенные преобразования Хо»… Определение степени родства этих материалов с настоящим исследованием и установление здесь авторского первенства – предмет отдельного разбирательства. К непреходящим же достоинствам настоящей работы можно отнести то, что вместо обычных обрывочных намеков и сакральных апелляций к высшей математике, даются смысловые – физические пояснения, которые и являются основой любой науки. Кроме того, все завязано в единую технологическую цепочку, показывающую место каждого концепта в общей задаче позиционного обнаружения – распознавания в целом.
sos