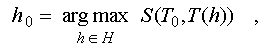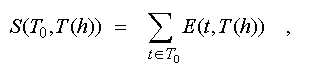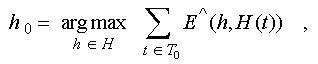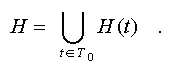3. POSITIONAL DETECTION VIA REGISTRATION
OF UNISON OF PARAMETRICAL HYPOTHESES.
Problem of contiguous
segment application as a base for solving of geometrical analysis problem
of following level - namally - jam-resistent positional detection of contour
figures of arbitrary sapes is considered.
3.1. - Essential Statement of the Problem
Of Positional Detection Via Registration of Unison of Parametrical Hypothesis.
3.2. - General Statement of the Problem.
3.3. - Comparision With Other Works.
3.4. - Main Particularities of Application
of Unison-Technique.
3.5. - Procedure Particularities. Results
of the Experiments.
3.6. - The Possible and Wanted Improvements.
3.1. ESSENTIAL STATEMENT OF THE
PROBLEM.
Let's make preciser the common sense
of problem statement of positional detection. Let us, it is a
triangle of the predicted form and sizes (fig.19a). It is
necessary to dispose the triangle on some picture so that
its elements will obtain a maximal confirmation by elements
of this picture. Let us, on the tested picture it is illustrated
same triangle only in other orientation (fig.19b).
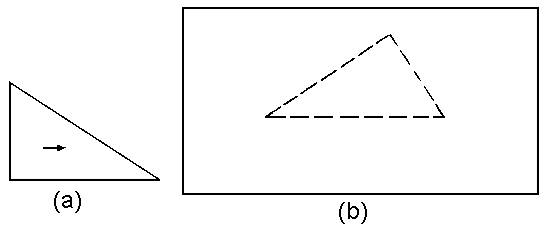
|
Fig.19a,b
|
We shall superimpose the
sample triangle on the analyzed picture each time juxtaposing
one of the sides with any contour segment of equal length. /
Besides individual segment will determine two possible juxtaposings
- one at each side. /
Obviously, that
in center it is obtained the multiple superposition (on
the number of the sides) of the reference triangle (fig.19c), that also
determines, in this case, the sought solution of problem of positional
detection.
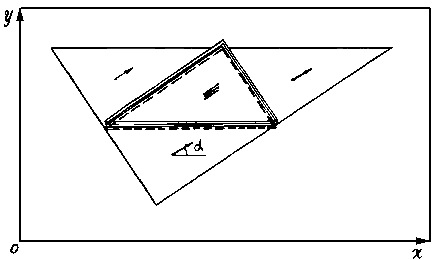
|
Fig.19c
|
This superposition
can be registered without any direct matching of contours
themselves. It is enough to draw on the reference triangle
some unit basis vector (see fig.19a), and register the superposition
of this vector (see fig.19c).
In turn, the
last problem is reduced to a search as much as possible marked
point of space of the parameters defining a position of a basis
vector on the analyzes image. Fig.19d illustrates the given situation.
On this picture the axonometric projection of space of defining parameters
is shown. In this case two parameters define coordinates of the
beginning of a basis vector, and one - an angle of declination
of this vector. Values of last parameter are registered on a vertical
axis.
Here the each marks is defined by a position of a basis vector
of a reference figure, at one of possible (initial) matching its
contours with an analysis picture.
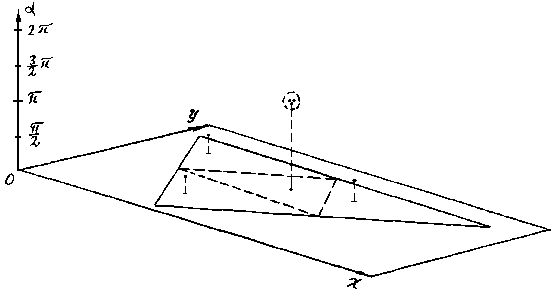
|
Fig.19d
|
It is obvious,
that registration of as much as possible marked point demands
essentially smaller computing expenditures, than direct examination
on coincidence of the standard of search object with an analysed picture
in the every possible positions generated independently by initial
juxtapositions.
Now we shall
return to our case, - when in the analyses picture initial
elements (contour segments) are detected not completely, but
in part (see fig.18a). In this case, to possible matchings of
the standard of a search figure with a separate (in part detected)
segment, will be corresponded to the line segment. This segment
represents the track left by the basis vector in the space of
parameters, during sliding of the standard concerning the separate
detected segment (see fig.18b,c). The search position, i.e. a position
in which the sides of the standard cover the greatest amount
of the detected segments corresponding a search figure, obviously,
will be determined by the point of the most powerful intersection
of the generated segments in a base space.
And at last,
in case of objects of the curvilinear form, to possible matchings
of the search figure standard to a separate approximating (contiguous)
segment, some curve of the space of determining parameters will
correspond, and to a search position - intersection of such curves.
Particularly, the positional detection process in this case
represents the following sequence of operations. The whole undistorted
image of search object (fig.20a) is registered. To this image - to
the standard - it is assigned a unit - basis - vector. For
a determinacy it is possible to consider, that as an attachment point
of the barycentre of a contour of the standard (though it is not
necessary) is chosen.
|
Fig.20
|
Then, along a contour
of the standard some formal approximating (contiguous) segment
(with continuous fine tuning branches) compulsorily moves ahead.
During such movement - slidings - the position of the standard
(its basis vector) in own frame (bOd) of the sliding formal
segment (fig.20b) is registered. The set of the obtained collections
of parameters represents some reference generated curve.
The axonometric projection of the space of determining parameters
for this case is shown on fig.20c. Here on the vertical axis the
angle between the basis vector and the longitudinal axis of segment
Ob is registered. Points of the obtained curve show possible positions
of the standard of the search figure (an its basis vector) concerning
a separate approximating (contiguous) segment.
In the process
of the positional detection itself, the reference generated
curve sequentially is juxtaposed with each segment detected
on the analyses image. Such juxtaposition represents juxtaposition
frames of the reference curve with a segment frame and the subsequent
translation of its points in a frame of the parameter space defining
a position of the basis vector on the analyses image. Thus to values
of angles the declination value of a flowing segment is added.
Now points of each generated curve show, what positions the
standard of search object (its basis vector) concerning the given detected
segment can occupy at sliding the standard with the contour on this
segment.
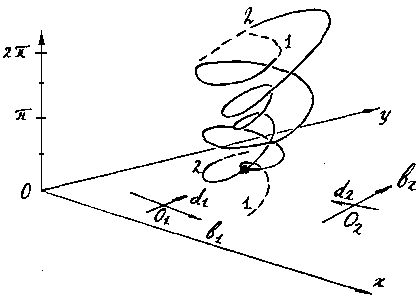
Thus, the problem
of positional detection of flat objects is reduced to the
search of intersections of the similar curves corresponding to
individual approximating segments. An example for two segments
is shown on fig.21. Here xOy - a frame of the image. On the vertical
axis the angle between the basis vector and horizontal axis Ox is
registered.
|
Fig.21
|
The cross point
of the majority of the generated curves defines such
position of the standard of search object (its basis vector)
at which the contour of the standard simultaneously coincides with
the greatest number of the detected segments. It, obviously, also
is a solution of the considered positional detection problem.
It is necessary
to note, that the considered algorithm does not assume an
obligatory continuous smoothness of contour boundaries of search
objects. For serviceability of the algorithm it is necessary,
that the number of singular points of these boundaries (angles)
was finite. Objects should not remind a hedgehog or
a cloud. Presence of separate smooth pieces is required only.
It, as a rule, is ensured with the process engineering of operations
on shaping objects: cutting, planing, grinding, stretcting, forging,
etc., and also the physics of the nature: forces of inertia,
a superficial tension; regularities of processes of cleaving, cracking,
etc., etc. The reference curve is under construction on such smooth
pieces and represents set of separate curves (space of search parameters),
corresponding these pieces.
Also absence
on the analyses image of separate parts of the contour boundaries
corresponding to the search object is obvious, that does not
render a fatal influence on outcome of a positional detetion.
In that case only a potency of a search cluster accordingly will
decrease.
3.2. GENERAL STATEMENT OF
THE PROBLEM.
To compare the
suggested positional detection procedure to already available ones,
to show its place among them, and also to offer possible expansions
of the use domain, we shall give a formal statement of the detection
problem by means of registration of an unison of parametrical
hypotheses.
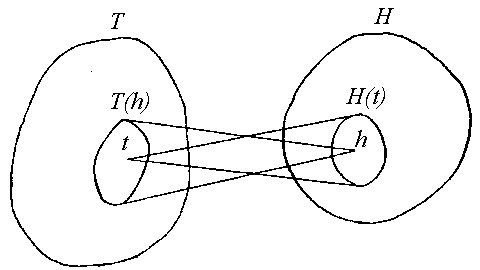
Let there is
a set of hypotheses H about some physical phenomenon and
a set of facts T which can be registered at research
of this phenomenon. Thus it is known, that each hypothesis h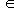 H is confirmed by the defined subset
of facts T(h)
H is confirmed by the defined subset
of facts T(h)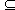 T. Further each such subset we shall
name a factogram (factograph) of the given hypothesis.
T. Further each such subset we shall
name a factogram (factograph) of the given hypothesis.
Usually, the
problem of a hypothesis choice h_o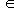 H, corresponding to some set of facts T_o
H, corresponding to some set of facts T_o T, further named a set of the realized facts,
is put and solved as a problem of searching of a hypothesis
which factogram has a maximum conformity with this set:
T, further named a set of the realized facts,
is put and solved as a problem of searching of a hypothesis
which factogram has a maximum conformity with this set:
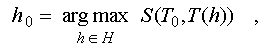
Where
S - the
function defining a conformity between sets of the facts.
In the simplest
case the conformity is defined by number of the elements
simultaneously belonging to both compared sets:
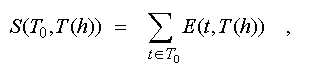
Where
| E(t,T(h))
= |
1, if t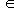 T(h);
T(h);
0, if t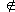 T(h).
T(h).
|
It is possible
to tell, that in this case it is prospected the hypothesis CONFIRMED
by a maximum quantity of the realized facts.
Now we shall
remark, that the same problem of search of the hypothesis corresponding
to the realized facts, it is possible to put as a problem
of search of the hypothesis GENERATED simultaneously by the greatest
amount of these facts:
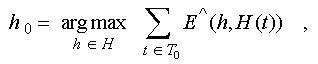
Where
H(t) =
|
{h|h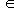 H,t
H,t T(h)} - a subset of the hypotheses generated
by the individual fact, i.e. confirmed by this fact. Further
each such subset will refer to as a hypogram (hypograph) of the
concrete fact. Fig.22 picturesquely illustrates the essence of
introduced concepts.
T(h)} - a subset of the hypotheses generated
by the individual fact, i.e. confirmed by this fact. Further
each such subset will refer to as a hypogram (hypograph) of the
concrete fact. Fig.22 picturesquely illustrates the essence of
introduced concepts.
|
| E^(h,T(t))
= |
1, if h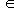 H(t);
H(t);
0, if h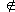 H(t).
H(t).
|
|
Fig.22
|
Namely this sense
is put in the concept of search by means of registration of an unison
of parametrical hypotheses.
Before such kind
of search named as search by a principle of accumulation of hypotheses
[3]. The modified name reflects the
essence of the process more precisely. The former name concerns
to particularities of realization. The considered statement
of the search problem naturally leads in its realization, based
on use of some set of accumulators, isomorphic to a set of sorted
out hypotheses. In this case each next fact is taken into account
one time, by a mark of accumulators which correspond to the hypotheses
which are included in a hypogram, generated by this fact. After
the termination of search of all facts and marking of accumulators
it is necessary to register an accumulator having a maximum number
of scores. This accumulator also defines, on a new nomenclature,
the unison - consent of the generated hypotheses.
Comparing the
first and second kinds of search, first of all it is necessary
to tell, that outcomes obtained with their help are in essence
equivalent. It is caused by that an amount of confirmations of
any hypothesis obviously equally to number its generations.
Rationality of
use of this or that hypothesis search mode corresponding to the realized
facts, depends, first of all, on a mode of definition of a set of hypotheses
H subject to examination. Advantages of the technique of accumulation of
hypotheses appear indisputable when hypotheses are directly generated by
individual facts on which examination of these hypotheses, namely when the
set of hypotheses is defined as is made also:
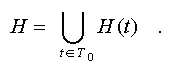
In this case
there is no repeated return to already overlooked facts expressing
in evaluation of the conformity function.
If character
of a problem allows to limit somehow number of hypotheses in comparison
with what is generated by all realized facts separately (that
rather frequently takes place) expenditures on designing of
an accumulator can appear unjustified. In this case it is possible
to be limited to direct examination of confirmation of the
factograms corresponding to the available hypotheses. It is necessary
to take into account concrete particularities of a decision
problem.
At a solution
of the positional detection problem, the role of the facts
is played with separate elements of analysis images. These elements
- initial features, under the supposition, correspond to some
elements (fragments) of search objects. Each initial feature chosen
in an analysis picture, generates a set of hypotheses about parameters
of the search object, i.e. a hypogram. Thus to each hypothesis
the point of space of the parameters defining a position and orientation
of object corresponds, and to an individual hypogram - the defined
set of such points. Further for simplicity these point sets will
refer too as hypograms. The search position of object is defined by
a cross point of hypograms. Naturally, generally it is necessary
to speak about this point as about a point of a cluster (clusterization),
i.e. about a point in which neighbourhood the greatest number of hypograms
hits.
3.3. HYPOTHESES UNISON
IN THE POSITIONAL DETECTION.
The positional detection algorithms
based on the cluster analysis of the space of search parameters, draw
attention of experts on visual recognition of objects. The majority
of researches of this direction goes back to the widely known Hough
transform [7, 20 - 27]. The essential shortage
of these algorithms consists that the search parameters are considered
as parameters of some abstract transformations of the elements
of the reference image into similar elements of the analysis image
[22, 25]. Such statement of a problem hampers
understanding of logic of build-up and further improvement of
similar detection algorithms. In particular, it leads in enough
abstract reasonings on "collinearity" of contour points [7, 28]
or about "not dot transformations" [21, 22]. It is necessary to prove
equivalence of the outcomes obtained with the help of these algorithms
and recognition algorithms in which basis comparison with
the standard [29] lays.
The substantial
approach to positional detection problem as to a search
problem of superposition of modelling images of the search objects
generated independently by individual fragments (features) of
these objects [19], directly suggests
parametrization methods. Obviously, as the search parameters it
is necessary to use parameters of the simplest configurations of
structural elements rigidly connected to the standard of search object
and permitting completely to define its position and orientation. Thus,
the essence of the detection problem is reduced to search of superposition
of such configurations. In the case of flat objects a basic configuration
is any unit vector assigned in the beginning to the object standard. If
the scale changes, respective variation of length can be assigned to this
vector. In the case of 3D bodies two unit vectors starting from one point
can be a basis structure. The position of such structure is determined by
six parameters: three ones set coordinates of the attachment point, two
ones - orientation of a principal vector of this design, and one parameter
- rotation of an auxiliary vector around of principal one. It is possible
to use the Eulers angles. In this case the basis strucure will represent the
thriplet of mutually perpendicular vectors which are starting from one point.
In all these cases an individual hypogram will be defined by set of positions
of the basic structure which it can occupy concerning the given initial feature
(fragment) of the search object.
The suggested
ontological scheme represents generalization and attempt of more
deep clearing up of the essence of similar algorithms. First of all,
this scheme directly shows equivalence of the outcomes obtained with
the help of this or that technique of object positional detection. A
vivid example of it is work of a matrix decoder which can be
considered and as parallel comparison with the standard (set
on the address register) and as search of intersection (cluster
cells) of hypograms assigned to address buses. It is necessary
to note, that the Guzman idea about promotion of global hypotheses
on the base of local data have served as initial push in the direction
of idea of accumulation of hypotheses [30], and the Walts idea of about
search of a consistent (compatible) mark of contour edges [31] - for the idea of superposition
of models .
Probably, the
proposed ontological scheme will serve further movement to understanding
of the essence of various search kinds and correlation between
them. The considered example, where the hypothesis choice is carried
out with simple calculation of binary voices, reflects only the
simplest case. A purpose of this example - to show basic equivalence
of indexes of confirmation measure and measure of generationess
of hypotheses, in the simplest case - the binary count of the facts.
Generally the membership functions can have more complicated view:
to accept a continuous spectrum of values (for example to be fuzzy),
to accept negative values (individual facts can refute some hypotheses),
etc., etc.
3.4. MAIN PARTICULARITIES
OF APPLICATION OF UNISON-TECHNIQUE OF POSITIONAL DETECTION.
Further, the technique of positional
detection based on registration of unison of parametrical hypotheses will
be named also simply as unison-technique (unison-detection ets.).
Use prospectivity of thise technique in comparison with the technique
of direct examination of hypotheses confirmation, which in this
case can be named examination on conformity with models-standards,
depends on concrete particularities of the problem solved.
The technique
of direct examination on conformity with models is efficient when
the search of small amount of hypotheses is required, for example,
when there is a possibility of efficient detection of the high
informative fragments essentially bounding a set of generated
hypotheses or when character of a problem allows to apply any strategy
reducing search. In particular, it concerns to the case when the
conformity measure on an admissible set of hypotheses is the smooth
function having limited number of extremums. In this case for search
of its maximums it is possible to use gradient procedures. Such search
strategy, for example, is applied in the proposed representation
mode of contour boundaries in terms of contiguous segments.
In those cases
when on a problem there are only low informative initial features
(facts), each of which separately poorly limits an amount of
admissible hypothesises, advantages of the hypotheses accumulation
technique can appear resolving. As here, instead of multiple
and, as a rule, protracked evaluation of the conformity function,
a simple coincidence of points in own space of hypotheses
is registered.
As well as by
search, in which base evaluation of the conformity function lays
(search by principle of direct hypothesis test), the choice of
initial features is a key defining boundaries of applicability of hypotheses
accumulation technique. If to use the most universal initial features
- contour points [20 - 22], computing
resources of modern computers allow to solve practically only the problem
of positional detection of two-parameter objects (in particular, infinite
straight lines).
To limit number
of generated hypotheses up to a comprehensible level, at the
solution of more complicated problems of geometrical detection
(with a big number of unknown parameters) it is necessary to use more complicated
initial features (fragments) of search objects too. The basic difficulty
thus will be, that the following on the complexities, the most natural
initial features, - the rectilinear contour segments connecting points of
inflection - sharply limit a class of recognition objects. As it was already
marked,it is impossible to divide univalently the contour boundaries of the
objects having smooth contours (fig. 20a) into separate segments. Approximating
segments on such contours generally cannot be fixed legiblly enough. Thus,
each segment generates rather extensive - sliding - set of possible
positions of the search object. Here by the best way of detection by the registration
of unison of parametrical hypotheses proves.
The basic difficulty
at realization of such positional detection algorithm consists
in necessity of steady definition of orientation and cross position of
sliding approximating segments in the case of real curves,
when these curves are set discretely and deformed by various interferences.
If to define
these directions by short segments (to provide common universality
of the algorithm, irrespective of the form of objects), in real
conditions casual oscillations of these segments will lead to
essential oscillations of the base vector. For example, if to
use contour elements obtained directly with the help of the Hueckel's
operator [5, 6] (as it was offered
in [23]). In this case, oscillations
of the ends of obtained elementary contours with an amplitude plus or minus
one point, at diameter of the entering piece in 7 points of the raster,
on the distance of 50 points (that corresponds to average distance up to
the center of a figure in diameter in 100 points), lead to oscillations
of the basis vector with amplitude of 15 raster points (50/(7/2)).
In this case
it is necessary to hope only that the searched correct solution nevertheless
will turn out due to statistical averagement. Such solution
assumes the organization of the count of a great numbery of the
hypograms generated by individual elementary segments. The extended
machine memory for storage of a hypotheses accumulator is required.
Significant expenditures of machine time for the procedure of
hypotheses accumulation and the analysis of the obtained (in an
accumulator) pictures are necessary.
On the other
hand, the suggested in [25]
sliding matching on extended pieces of contour lines basically can
satisfy stability requirements. However, it does not ensure universality
as it is limited only to the case of rectilinear segments. Though
and for this case here it is necessary to expect essential difficulties
owing to absence of an effective mode of segment approximation.
In the proposed
scheme of realization of unison-procedure the sliding segments,
which are simultaneously meet the requirements of universality
and stability, namely - contiguous segments, are used. Virtues
of these segments are defined by that the use of bell-like memberships
functions included in their basis allows to tune out effectively
from jamming. Bell-like function enables correctly - on a maximum
- to lean on length of juxtapositioned contours.
As the result,
it was possible to construct an jam-resistant, costructivelly realizable
procedure of positional detection of arbitrary form objects.
3.5. PROCEDURAL PARTICULARITIES.
RESULTS OF EXPERIMENTS.
The proposed positional detection algorithm
has been realized in the language FORTRAN (a small part
- on the autocode).
Build-up of a reference hypogram of the search object is carried
out under its full undistorted image. As an attachment point
of the basis vector the barycentre of contour boundaries gets out.
During build-up of a reference hypogram the step of movement of
a formal contiguous segment is continuously arranged with the help
of feed-back so that to keep adjacent points of a reference hypogram
within the limits of one zone into which the space of search parameters
is supposed to divide. This space is represented as set of rectangular
zones.
The size of zones
on an axis defining declination of a basis vector, gets out according
to a condition of approximate equivalence of shift ( L) and turn (
L) and turn ( A) a reference figure:
A) a reference figure:  A=
A= L/R, where R - radius of object. This value
is calculated as arithmetic mean lengths of the radiuses - vectors
directed from a barycentre to each points of contour boundary.
L/R, where R - radius of object. This value
is calculated as arithmetic mean lengths of the radiuses - vectors
directed from a barycentre to each points of contour boundary.
Hypograms of
the contiguous segments detected on the analysis image are obtained
by "juxtaposition" to them of a reference hypogram (thus
coordinates of its points are accordingly transformed).
Hypograms are
set pointelly with a step commensurable with linear sizes of the
zones. Therefore, marking in the intersection field of several
hypograms can not give one zone which would be marked
simultaneously with all these hypograms. To overcome similar
accidents of a discrete mark, in the program realizing the algorithm
the averaging of obtained pictures is made within the limits of adjacent
zones. For each marked zone its weight - the arithmetical sum
of contents of adjacent zones - is calculated. Contents
of the zone are a number hypograms marked it. 27=3x3x3 zones are
considered as adjacent, including central one. The separate cluster
is registered as a zone which weight exceeds weights of the neighbours.
The central point of such zone starts a cluster point. As a whole,
such operation is called as smoothing.
In the program
realizing the algorithm, the information only about marked zones
is remembered. For this purpose some array is assigned. The
entry is executed with the help of hashings [Appendix_3.5.A].
Reference hypograms
of recognition subjects - insoles, an iron and a case from
glasses (see fig.13) - were constructed on their separate images.
The sizes of search parameter space zones on the axes defining
a position of an attachment point ( L) was equal to eight (8) points of the raster.
On the axis defining declination of the basis vector (
L) was equal to eight (8) points of the raster.
On the axis defining declination of the basis vector ( A) it was equal 0.1 radians. The linear size
of the zones got out approximately equal to a minimum distance
on which two parallel contours are distinctive. In this
case this distance - solution - was defined by the diameter
of entering area of the Hueckel's operator with which help elements
of contour boundaries were selected. Diameter of this area was
7 points of the raster [2.2.]. The concrete value "8" has been chosen
as the nearest power of 2, that essentially accelerates
operation of definition of the zone number (instead of division - shift...)
. The angle sizes of zones according to above indicated equivalence
criterion of shift and turn for figures with average radius of 50 raster
points (average radius of objects in this case).
A) it was equal 0.1 radians. The linear size
of the zones got out approximately equal to a minimum distance
on which two parallel contours are distinctive. In this
case this distance - solution - was defined by the diameter
of entering area of the Hueckel's operator with which help elements
of contour boundaries were selected. Diameter of this area was
7 points of the raster [2.2.]. The concrete value "8" has been chosen
as the nearest power of 2, that essentially accelerates
operation of definition of the zone number (instead of division - shift...)
. The angle sizes of zones according to above indicated equivalence
criterion of shift and turn for figures with average radius of 50 raster
points (average radius of objects in this case).
At such zones
sizes of reference hypograms of the search objects contained accordingly
85, 60 and 45 points.
During accumulation
of hypotheses about an insole position (on fig.13), 1784
zones have been marked. From them: fourfold - 1, threefold -
3, twice - 47, one time - 1733 (time of accumulation of hypotheses
1,5 s; computer
efficiency - 1 million operations from a floating point). Among these zones after
operation of smoothing 18 separate clusters (smoothing time
1,0 s) have been registered. Relationship of weights of these clusters
is shown on fig.23.
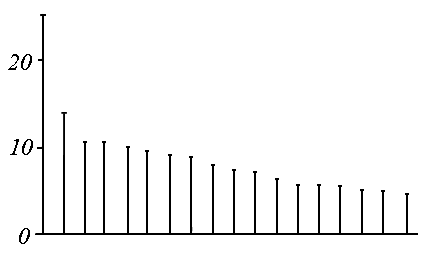
|
Fig.23
|
Histograms of
maximum weight zones of the most powerful clusters are shown on
fig.24.
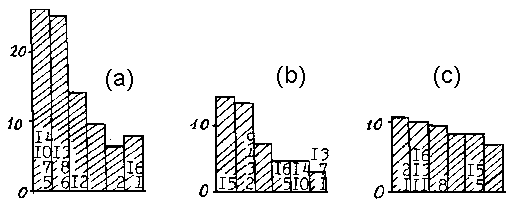
|
Fig.24
|
Each histogram
shows values of the most powerful zones situated on various distances
from the central zone. Distances are registered on horizontal
axes and measured in terms of a digitization step. Numbers of
the hypograms for the first time appearing on the given distance
are present on the histograms. Indexing of segments see fig.25.
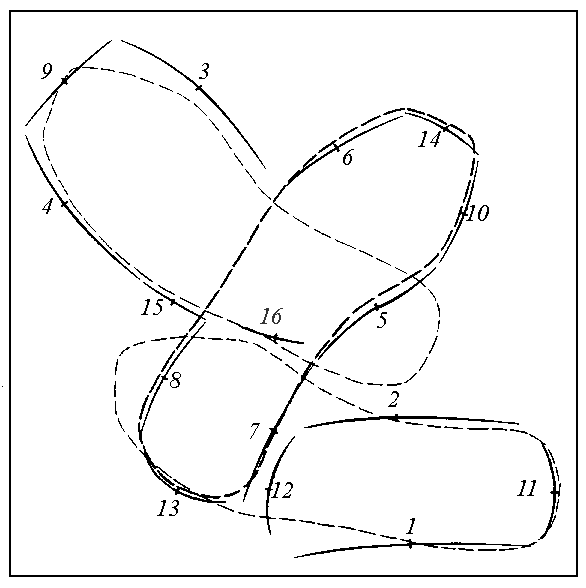
|
Fig.25
|
On fig.25 fat
primes show the position of the standard of the search object, defined
by the central zone (the central point of this zone) of the most
powerful cluster (fig.24a). On the same picture thin primes show
positions of the standard, defined by two most powerful false
clusters (see fig.24b,c).
In [Appendix_3.5.B] the problem of common
expediency of smoothing operation is considered.
Experiments were
carried out with various variants of disposition of contiguous segments
on the contour boundaries of search objects. At attempts to fix contiguous
segments on represantation contours [2.4.] the most various dispositions
of these segments were obtained. In particular, for an insole it has been
analysed about ten variants, which include approximately 70 (7 segments
X 10 variants) different positions for a separate contiguous segment (including
the most unsuccessful, corresponding to the pieces of significant
curvature). In all these cases the point of parameter space corresponding
to the true position of the search object on the flowing image was
in the central zone of the most powerful cluster. Thus all hypograms
generated by segments contiguous to a search object contour hitted
(by any points) if not in this zone, in the last resort in one of
adjacent zones.
The experiments
carried out in this way have confirmed basic serviceability of the considered
positional detection scheme of arbitrary form objects and have
shown a possibility of its to constructive realization.
3.6. THE POSSIBLE IMPROVEMENTS.
The accepted concept of equivalence
of contiguous segments is intended for the worst situation - a case
of very smooth contours, with feebly marked changes of curvature.
Naturally, in general case at matching of contiguous segments it is
necessary to take into account, even roughly, parameters of their branches.
With all evidence it is shown with exibited examples of false situations
of the search object (see fig.25). If the insole heel is approximately
entered in the contiguous segments representing a glasses case contour
and an its nose - in an iron contour, confirmation of the rectilinear
piece of contour boundary of search object by curvilinear segment N~13
and the curvilinear piece by rectilinear segment N~2 only on the basis
of their mutual tangency evidently is not justified. Organization of
hierarchical count of hypograms, i.e. accumulation of hypotheses by way
of their probability is a problem of further researches. And this problem
has a basic value as thus the relative weight of false cluster points
should decrease considerably.
Research of the
problem of use of configurations of initial matching (initial fragments)
built of several (first of all from pairs) adjacent contiguous segments
seems to be rather prospective also.
For reduction
of computing expenditures by the hypotheses accumulation principle
it is possible to make search iterativelly: initially to work
with big zones and rough representation of hypograms and then to
analyze intersection zones using more precious representation and
smaller zones.
Other mode of
reliable registration of hypogram intersections (without use of smoothing)
consists in marking of all tops of each zone. At increase of
dimension of the space of search parameters expenditures in additional
memory can appear smaller than on an evaluation of the local (neighboring)
sums. In this connection it would be expedient to solve the problem
of subdivision of space of parameters into zones having a minimum
number of tops (for two-parameter space they are triangles, for three-parametrical
one - tetrahedrons, etc.).
Naturally, realization
of the suggested scheme can appear too bulky for direct
positional identification of complicated objects, i.e. objects which
contour boundaries demand for their description about ten and more
contiguous segments. Here the suggested scheme can be applied to detection
of separate fragments of such objects used further for a final geometrical
detection problem solution with the help of structural methods or subsequent
direct matching of models (standards) of search objects with
analysed pictures. As a whole, in detection of such fragments already
enough legiblly corresponding to separate parts of actual objects
it is possible to see the basic applicability of the suggested scheme.
It is possible,
that the count of more thin performances of contiguous segments
and also improvements of realization technics of the identification
scheme will enable to spread its to positional detection of 3D bodies on
their images, anyway their fragments. Thus, for restriction of
volume of hypograms a use of the contiguous ("sliding") surfaces
describing a distance image essentially would help. This description
can be obtained as a result of the analysis of half-tone pictures,
methods of stereosight or direct mesurement of distance (for example,
using laser technics).