
Fig.1A
| Russian |

|
|
Fig.1A |
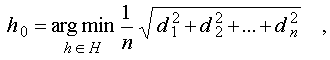
| h -
|
the parameters determining
the position of a segment; |
| H - |
area of admissible values
of parameters h; |
| n - |
the number of points
of an approximated set; |
| d_i - |
a deviation of an isolated
point from an axial line of a segment (fig.1B). |
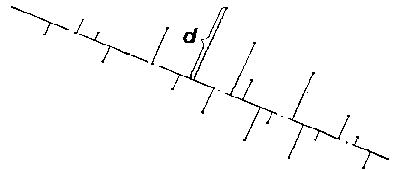
|
| Fig.1B |
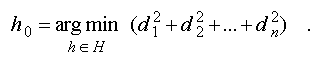
|
|
| Fig.1ab |
|
| Fig.1c |
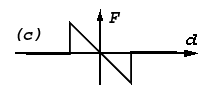
Outcomes of
approximation are very sensitive to a choice of a threshold of a maximum
deviation. In practice it is impossible to choose a threshold of the maximum
deviation at which simultaneously there would be no the false subdivision
of approximating segments caused by casual ejections, or cuts (averages)
of not clear expressed angles of analysis contours. The outcome of application
of root-mean-square approximation with threshold restriction of the maximum
deviation [1] is shown in figure below.
Here it is possible to find examples of both situations. And this best, that
it was possible to obtain.
|
| Fig.10c |

|
|
|
| Fig.1cde |
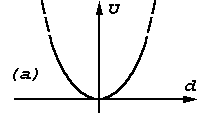
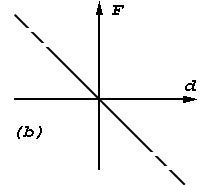
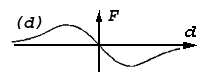
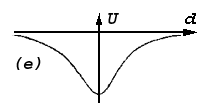
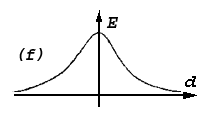
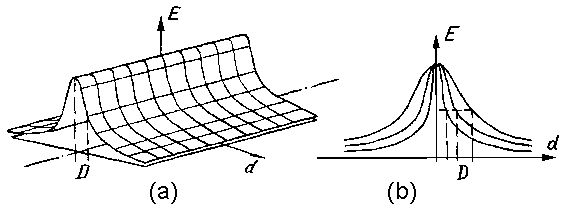
Inverse bell-like function may be obtained directly from parabolas also (fig.1a), – by "unbending" of its branches to some horizontal "ceiling". It is on the base that fare points must be equally indifferent ones. / Such it was obtained in primary. / The application here the force – differential interpretation enables more distinctly to formulate the problem and explain essentiality of its solving. Instead of reasoning about some "ceiling" it is defined that force attraction must have tendency to zero under increasing of deviation. Force interpretation too more stringently explains approximation role of central part of potential curve (of "parabolas rest" – "potential pit"). Instead of (in addition to) reasoning about that points must "roll down on its bottom", here it is giving direct representation about attracting force – it must be inversely proportional to deviation with changing of sign in pass through zero. In frame of force interpretation it is logically easier linked root-mean-square approximation and threshold admittance of allowed deviation. It is shorter passing from threshold admittance to gradual one. All these allowed to speak about expedience of application of force interpretation for explain of approximation problem.Now we shall return the approximation problem from field of physical representations to its initial geometrical "surrounding". In geometry it is mote naturally to consider points located closer to an approximating image (closer to axial line of an approximating segment) with more "weighty - valuable", and - on the contrary farther - less "valuable". To result physical interpretation in conformity with this position it must be "inverted". At first, it is necessary to pass from invert bell-like function to direct bell-like dependence (fig.1f).
|
| Fig.1f |
It is possible to reach a bell-like membership function also directly by "smoothing" – "melting" ofGeneral statement of the approximation problem based on smoothly limitation of influence of remote points further is given. The place of such approximation among procedures of structural representation of linear images is considered.-like – threshold function. However, additional explanations about the functional roles of various pieces of this "smoothing" are needed. First of all, it is necessary attention to approximation role that begin to play center – top of such “smoothing”. All these roles are directly illustrated by force interpretation. The force interpretation links together the operation principles of root-mean-square approximation, threshold limitation of permissible deviation,
-like membership function and their development – bell-like estimation of this membership. The force interpretation instead of a series generally accepted "reservations" gives here descriptive - force - causal "section".
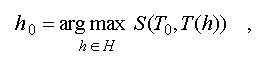
| h
- |
the parameters defining the position and orientation of a segment(generally, and its shape); |
| H
- |
area of admissible values of parameters h; |
| T(h)
- |
subset of points
of images, belonging to individual approximating
segment (some ideal image of this segment, - "band"
of points ambient its axial line); |
| T_o
- |
set of contour
points detected on the image; |
| S
- |
measure of geometrical conformity of T(h) set (image) to T_o set. |
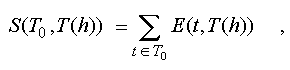
|
| Fig.2 |
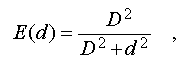
Where
| d
- |
value
of a deviation from the axial line of an
approximating segment which position is defined by
parameters h; |
| D
-
|
defines
a deviation at which the value of function of a membership
decreases twice (further the double value of such deviation
we shall name its width). |
The cross-section
of a set of the bell-like functions defined
by this expression is shown on fig.2b.
Further alongside
with the term bell-like we shall use
also the term fuzzy, proposed in [4] as a generalizing
title for a similar sort of functions.
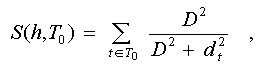
Were
| h - |
parameters defining a position
of an approximating segment, |
| T_o - |
a set of chosen contour
points, |
| d_t - |
a deviation of the point
- t from an approximating segment. |
Thus, mathematical
expression of such measure, for a case of
approximation by straight lines, is defined as
follows:
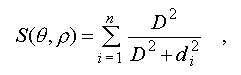
Where
| declination of the perpendicular
radius-vector let down from the center of
coordinates on an approximating line (fig.3a),
|
|
| length of this vector, |
|
| d_i - |
a deviation of i-th contour
point from the axial line = x_i * cos( |
| x_i, y_i - |
coordinates of a point, |
| n - |
number of contour points.
|
Hereinafter
in terms of a conformity measure we shall omit (implying its presence) parameter
T_o designating a set of contour points.
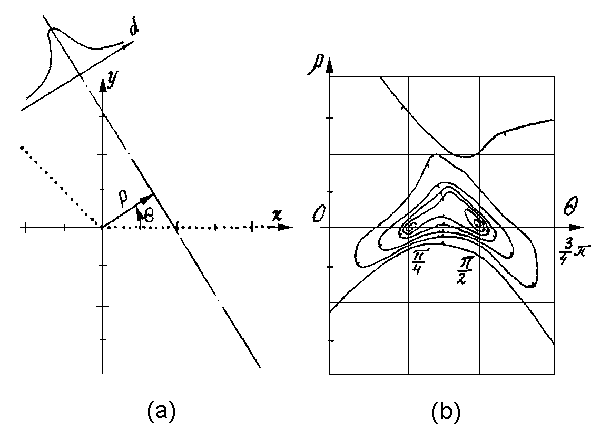
|
| Fig.3 |
Therefore, in
general the desire to remain, whenever possible,
within the framework of the problem solution (i.e finding
of the minimum of a pure root-mean-square deviationis)
is natural.
However, the
minimum of a standard deviation as it has been shown,
inherently reflects globally averaged conformity of
the model (a tried on pattern) with analysis pattern. In
this case the conformity measure monotonically decreases
with increase of a deviation of any element of the analysed pattern
from a corresponding element of the tried on model.
Derivation of
the adequate description of any picture with the
help of such conformity measure can be obtained
only in a case when among compared models there is
a model of all analysed pattern. In this case, minimizing
a summarized deviation, we can obtain search outcome, i.e.
to find a corresponding model. Otherwise, we shall obtain
an averaging of an analysed pattern of one of available
models that can not have anything common with necessary outcome
- an adequate description of the given pattern or even of
its part.
Effectiveness
of use of the criterion of summarized (root-mean-square)
deviation directly depends on as far as we can legiblly
select an approximated pattern from its environment or
as far as we can fully reflect an analysed picture with
any integral model. From this viewpoint it is possible to select
two approaches in a solution of the problem of the description
of pictures of various kind on the basis of minimization of
a root-mean-square deviation:
- Sequential
independent detection and approximation of individual
included as the parts in the analysed picture [1, 5,
6, 13], in particular,
of separate segments of contour boundaries.
- Approximation
of input data with integral models (see, for example,
[8 - 12]), in particular, contour
boundaries with chains of segments;
Adequacy descriptions
obtained on the basis of last approach to theanalysed
pictures is ensured, first of all, with that here elements
(points) of input data in a result will be distributed
between corresponding elements (segments) of tried on
models and will not render so negative towing away influence
on adjacent elements (segments) of the tried on model. For example,
if to approximate an angle (see fig.1A, fig.3) with a corresponding
integral model (a chain of two segments), basically, it is possible
to obtain an adequate outcome even within the framework of pure
standard approximation.
However, such
approach is effective only as fine tuning
when a priori there is an initial approximation - a model
already enough well reflecting an analysed picture, a
model which needs to be ajusted only. The prerogative
of definition of such initial models remains behind
the first approach - sequential contextual independent detection
and approximation of separate subpatterns.
In a solution
of this problem, in turn, also it is possible to
select two approaches, depending on a detection mode
of elements belonging to separate subpatterns:
- A priori
detection - unguided by tried on models during
approximation [5, 6,
13];
- Detection
controlled during approximation (see, for example,
[1]), - a rejection of the elements
allocated far from corresponding elements of the tried
on model.
A virtue of the
first approach consists that at its application the root-mean-square approximation
is used in the pure view, with computing simplicity implying from
here. However, such approach can be used only for representation of analysed
pictures with the simplest ones , i.e. with elementary patterns. These patterns
should represent adequately enough any arbitrarily chosen piece of a described
picture (anyway,the majority of such pieces). Such requirement can be satisfied
only for representation in terms of the simplest patterns were at a
discretization level of the representation of input data. For images
such elements are pieces of several raster points (about 5 - 10). Only on
such pieces, contour boundaries with an adequate accuracy can be described
by rectilinear segments - the simplest universal patterns in which terms
the arbitrary contour configuration basically can be circumscribed.
A virtue of the
second approach is the possibility to work with the extended patterns giving
more intelligent description of analysed pictures. However, in this case
the solution technics of the approximation problem becomes essentially
complicated. The problem becomes multiextreme, demanding basically for its
solution to use the initial approximations obtained outside of this approach.
Besides, an usual use of the threshold memberships functions leads to instability
of the approximation process...
And if the problem
of choice of initial approximations basically is
solved on the base of the first approach - detections
of the simplest patterns - the problem of incorrectness
of threshold rejection of outside points till now
practically was not solved.
Here the bell-like
(fuzzy) memberships functions play the main role.
Replacement of threshold function on the bell-like
one, at build-up of the conformity measure of approximating
models (segments) and described data (contour boundaries),
allows to loose criticality at definition of a
membership of elements of input data to an individual approximated
pattern. The bell-like memberships functions smooths
ruptures of the conformity function caused by discretization
of representation of contour boundaries, and also
by random interferences that allows to apply simple
gradient procedures at search of its extremums. Besides,expansion
of the foundation of searched maximums (caused by
branches the of bell-like memberships functions) causes smaller
criticality in a choice of initial approximations. Experiments
(including ones with actualon) have confirmed validity of
these ideads (see section 2.2.).
As a whole, the
analysis of particularities of various approaches to a solution of the problem
of approximation of contour boundaries leads to a conclusion about expediency
of their complex, sequential use. In the beginning, with the help of procedures
of pure root-mean-square approximation the contour image can be described
in terms of the simplest linear elements. Then, best of them (values of a
deviation defined by minimum values) should be used as initial approximations
for the subsequent procedure of maximization of the "gently selective" conformity measure, obtaining
in outcome the description with extended segments. Then, in a case of need,
it is possible to arrange parameters of these segments as an integral set,
redistributing contour points between them.
In conclusion
of this chapter it is necessary to point on common
methodological virtues of the concept of bell-like
- fuzzy - memberships functions. Basically, in the problem
of the description of real contours, application of probability
estimations of a membership of contour points to an individual
pattern [14, 15, 16] is
possible. However, as the experiments show, the statistical
model of contour boundaries (being the base of this approach)
in which signals are rectangular edges (ideal segments), deformed
by normal noise, is the theoretical idealization rather far from
the reality. Actual distortions of contour boundaries are various
curvatures, stains, extractions, etc. which count in statistical
models calls essential difficulties, and abstract from the essence
of the solved problem. The essence of this problem in this case
consists in leading an approximating segment on the axial
line of the representatede piece of contour boundaries, with correct
restriction of influence of outside points.
The solution
of the problem of description of contour boundaries
in terms of segments of axial lines as problems of search
of maximums of bell-conformity, with postulation of
fuzzy - bell-like memberships functions, seems to be
more fruitful, than designing of strict models of
researched signals. Thus, concerning these signals the most
common properties are assumed only, namely - a significant
sparseness of a set of segments of lines , each of which can
be deformed by individual ejections, curvatures, etc.
Told above it
is possible to supplement with the statement expressed
in work [17] : "... Inclining
of many contributors that the theory of statistical
solutions gives any more strict and objective classification,
than other algorithms of a decision making, is formalistic
fallacy... The objective measure (proximity) is not present
due to subjective character of statement of the problem of
pattern recognition... More important, evidently, is the problem
on simplicity of definition of of proximity (conformity)
measure...". For many problems there is enough to use concepts
of fuzzy (bell-like) memberships functions and based on it a measure of geometrical conformity, as, for example, in the
considered approximation mode of contour boundaries.
Thus, build-up and modification of procedures of segmentation-approximations
become much simpler.
For example, quite naturally the
necessary on the course of problem solution changes
of memberships functions width and illegibility of ends
of the approximating segments (see the subsequent sections),
are introduced naturally enough.
Deriving of any
strict analytical estimations describing these phenomena generally, is represented
rather by a complicated problem. Here, obviously, experimental researches
should play the principal role. As rough estimations it is possible to use
outcomes of the analysis of the simplest case, namely a case of two parallel
segments. The cross-section of the given picture is shown on fig.5a. The
position of segments here is determined by points x0 and -x0, and the position
of the axial line of an approximating segment is determined by parameter x.
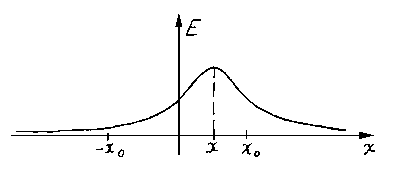
|
| Fig.5a |
The analytical
researches, which have been carried out on the basis
of proposed expression of function of a membership, have
shown, that the conformity function in this case has the
separate maximums corresponding two parallel segments if the
width of membership function has value smaller than the distance
between these segments, enlarged in sqrt(3) times (fig.5b).
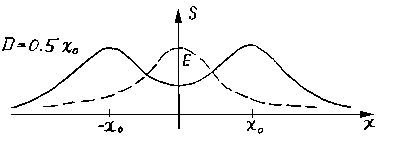
|
| Fig.5b
|
If it not so, the maximums
merge in one (fig.5c). The proof of this statement
is reduced in Appendix
1.6.A.
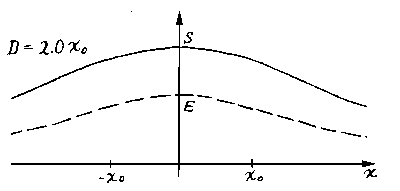
|
| Fig.5c
|
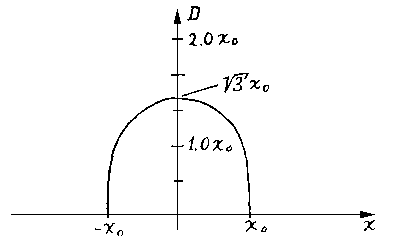
Positions of
maximums depending on a value of parameter D are shown
on fig.5d. In this figure to keep correspondence of the
horizontal axis to the previous figures, explanatory variable
D is registered on the vertical axis. The error of an estimation
of a position of search segments on maximums of the considered
conformity measure sharply decreases with decrease of width of the.membership
function. For example, already at D < x_0 does not exceed 0.1
values of distance between segments, and at D < 0.5*x_0 - 0.01
same values.
|
| Fig.5d
|
The exibited
outcomes of analytical researches allow to estimate
conditions of confluence of adjacent points of approximated
contours. At width of the membership function exceeding a
step of representation discretization of researched contour
segments more than in sqrt(3) times, the conformity function will
have one common local maximum for each two adjacent points, even
at transition of an approximating line is perpendicular to a
segment connecting these points.
Correction of
the membership function is suggested to be realized
by direct introduction of its width in the number of search
parameters of conformity measure and a use of such membership
function at which the amplitude at its width decrease will
increase (fig.6a):
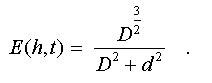
|
| Fig.6a |
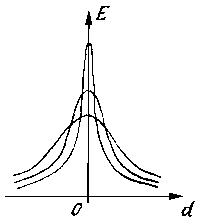
In a result,
the expression defining the conformity measure obtains
the following view:
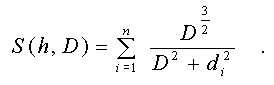
In this case,
at each fixed declination of the axial line, the local
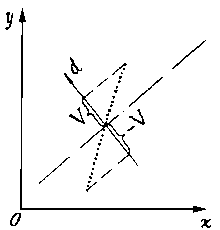
maximum of such measure is reached at D = 0.7*V, where
V - a relative half-width of a representation segment (half
of length its projections to a direction, perpendicular to a
flowing direction of the axial line, fig.6b). During search of
the next maximum of such conformity with decrease of a mismatch
between a represantation segment and the axial line a width of membership
function will decrease accordingly, ensuring thus a necessary
exactitude of definition of a segment position.
|
| Fig.6b |
Such measure
of a conformity feels a relative segment width.
It is related to that now, at increase of the width of membership
function simultaneously with increase of the
contribution of the remouted points in the value of conformity
function, the contribution of the points close to the axial
line decreases. And the equilibrium between changes of these
contributions occurs at a final value of parameter D, when the
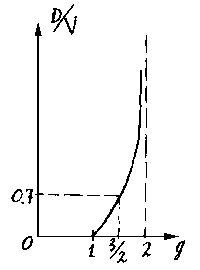
numerator in expression for the conformity measure of D\g (governing
growth rate of amplitude) has the exponent laying in an interval
1 <g <2 (fig.6c).
|
| Fig.6c |
Here the graph
of values of ratio D/V, at which the conformity measure
has the maximum value depending on parameter g, is shown.
This statement is proved in Appendix 1.7.A. In the given work the
value of an exponent g = 3/2 was used, that simplifies evaluations
and leads in steady tracing behind a relative segment width.
Thus, as it was already marked, D = 0.7*V.