2.3. Возможные усовершенствования

Программная реализация предлагаемого способа аппроксимации контурных границ прежде всего предназначалась для проверки ее принципиальной работоспособности. Организацию работы программы можно значительно улучшить.

Прежде всего представляются целесообразными дальнейшие исследования по оптимизации выбора величины шагов в процессе поиска максимумов нечеткой меры сходства. В рассмотренном варианте этот выбор осуществлялся на основе самых общих соображений (см. Приложение 4).

В настоящее время для выявления "ложных" ситуаций, возникающих в процессе поиска локальных максимумов нечеткой меры сходства (в частности, при захвате" нескольких отрезков), используется только итоговый, довольно громоздкий критерий заполненности получаемых прилегающих отрезков контурными точками. Для более оперативной оценки ситуаций, возникающих в процессе бел-аппроксимации, возможно использование информации о поведении градиентной процедуры - "характере" и числе шагов. Для этих же целей можно использовать взаимную согласованность (подтвержденность) аппроксимирующих отрезков, относящихся к одному и тому же участку контурных границ. Имеется в виду то естественное соображение, что если один прилегающий отрезок подтверждает своей ветвью поперечное положение и ориентацию центрального участка другого отрезка (и наоборот), то под этими аппроксимирующими отрезками скорее всего действительно находится совокупность контурных точек, соответствующая нашему понятию о едином отрезке линии.

Примененный способ предварительного выбора контурных точек рассчитан на работу в условиях полного отсутствия информации о топологических связях между отдельными элементарными контурами. Однако, как показывает опыт работы с реальными изображениями, контурные границы отслеживаются с помощью локальных операторов на довольно протяженных участках. В связи с этим представляется перспективным рассмотрение связанных участков контурных границ взамен изолированных точек из некоторой области. Кстати, это могло бы облегчить и аппроксимацию близко расположенных контуров.

Использование оператора Хюккеля для нахождения контурных границ анализируемых изображений обусловлено необходимостью упрощения экспериментов. По всей видимости, предлагаемый метод аппроксимации будет работоспособен и при использовании более простых операторов, например при использовании упрощенного оператора Хюккеля [18], оператора Собела, а возможно, и простейшего оператора Робертса [7]. Кроме того, просматривается возможность построения оператора, аналогичного по качеству результатов (и по сути, лежащей в основе функционирования) оператору Хюккеля, но гораздо более быстродействующего.

Основная доля счетного времени в процедуре выделения прилегающих отрезков затрачивается на последовательное вычисление вкладов контурных точек в текущее значение градиента меры сходства. Время работы процедуры можно существенно уменьшить, если эти вклады вычислять параллельно на специализированном вычислительном устройстве.

Все вычисления проводились в формате чисел с плавающей запятой. Нет принципиальных трудностей в их переводе в целочисленный вид. При этом "байтного" (или чуть большего) представления было бы достаточно в большинстве случаев. Резко сократить счетное время здесь позволит очевидная замена непосредственных аналитических вычислений на табличное задание колоколообразных (одномерных) функций и их производных. Необходимые при этом произведения также можно определять таблично. Объем таких таблиц, хотя и велик, но не превышает технических возможностей используемых вычислительных средств (для хранения этих таблиц требуется память порядка нескольких десятков килобайт).

В целом вполне реально увеличение скорости работы процедуры, представления контурных границ прилегающими отрезками, на несколько порядков.

2.4. Продольная фиксация прилегающих отрезков

Концепция прилегающих отрезков разрабатывалась как база для последующего распознавания-сопоставления контурных фрагментов произвольной формы в целом. С этой позиции, описание контурных границ прилегающими отрезками, которые отвечали бы участкам минимальной кривизны, выглядит предпочтительнее. Сопоставление контуров по таким участкам можно выполнить точнее, чем по "искривленным"; с другой стороны, такое описание естественным образом (если исходить из наших интуитивных представлений) разбивает контурные границы на участки с единичными вкладами в "вес" искомого объекта.

В этой связи экспериментальная проверка работоспособности процедуры представления контурных границ прилегающими отрезками выявила следующую проблему. Как оказалось, параболические прилегающие отрезки имеют тенденцию "наезжать" на плавные перегибы контурных границ. На рис.14 показан пример представления контурных границ, когда движение аппроксимирующих отрезков в продольном направлении осуществляется по направлению соответствующей компоненты градиента меры сходства.

Причем такой "наезд" обусловлен не шириной функции принадлежности, как это было в случае среднеквадратичной аппроксимации контурных границ прямолинейными отрезками. Во избежание возможного проявления "тонкостей" структуры функции сходства, вызванного прореживанием контурных границ, минимальная величина ширины функции принадлежности ограничивалась величиной, приблизительно равной величине шага между прореженными контурными точками (D = 1.5). Эксперименты показали некритичность получаемых результатов к выбору этой величины (пробные эксперименты проводились при D_min = 0.5 - 2.5).

Анализ этой ситуации позволил сделать вывод, что "наезд" здесь определяется самой формой аппроксимирующих кривых. Кривизна парабол максимальна в центре и уменьшается к периферии, поэтому параболы легко вписываются в такие участки контурных границ.

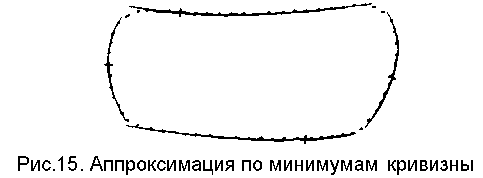
В работе [3] для ограничения "наезжающей тенденции" парабол было предложено двигаться в сторону ветви меньшей кривизны. Однако, как оказалось, при этом требуется противодействие "сползанию" прилегающих отрезков к концам представляемых участков при нечетко выраженных "максимумах прямолинейности" (рис.15). Корректно решить эту задачу не удалось, - не удалось однозначно подобрать какую-либо стратегию переключения продольной "движущей силы", которая позволяла бы одновременно избежать "сползания" аппроксимирующих отрезков и "наездов" на плавные перегибы.

В последней версии реализации процедуры аппроксимации контурных границ прилегающими отрезками было предложено "мягкое" ограничение ширины прямолинейных коридоров, которые могут занимать эти отрезки. Математически такое ограничение выражается в том, что при вычислении отдельных компонент градиента меры сходства контурные точки учитываются с весом, вычисляемым по формуле

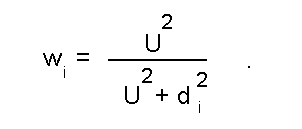
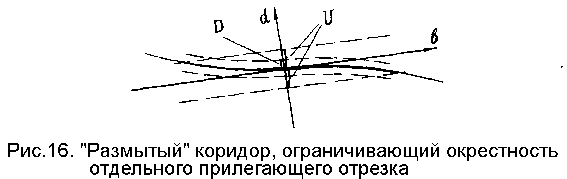
где d_i - отклонение i-й контурной точки от прямой линии, касающейся прилегающего отрезка в его центральной точке, т.е. от продольной оси его собственной системы координат; U - полуширина прямолинейного "коридора" занимаемого отрезком (рис.16).

Вторая серия описанных в предыдущем разделе экспериментов (их результаты показаны на рис.13) проведена с подобным учетом контурных точек, т.е. вклады этих точек в значения компонент градиента меры сходства умножались на их веса с учетом ширины допустимого коридора. При этом для вычисления компоненты, отвечающей движению в продольном направлении, использовался коридор с полушириной, равной 2.5, а для всех остальных компонент - коридор с полушириной, равной 5.

Плавное ограничение ширины прямолинейных коридоров, занимаемых прилегающими отрезками, позволило избежать их явных "наездов" на плавные перегибы и "сползания" к концам представляемых участков.

Вместе с тем, и здесь четкого решения задачи продольной фиксации аппроксимирующих отрезков получить не удалось. При использовании ограничивающих прямолинейных коридоров отдельный аппроксимирующий отрезок может потерять чувствительность к концам представляемой контурной линии, если эта линия имеет достаточную протяженность и кривизну, и потому может выйти за продольные границы ограничивающего коридора (увеличивать же ширину коридора нельзя, - начнет сказываться тенденция параболы наезжать на плавные перегибы). Примером таких контурных линий являются контурные ганицы отвечающие пятке стельки (рис.13), а также боковым сторонам утюга, когда контуры этого объекта представлены достаточно полно (рис.17).

В подобных случаях аппроксимирующие отрезки приходилось фиксировать произвольно-принудительно. Механизм такой фиксации состоял в том, что продольное движение аппроксимирующего отрезка в одну сторону разрешалось делать только на половину расстояния между двумя точками, в которых произошло изменение направления движения (вначале эта величина задавалась равной диагонали анализируемого изображения).

Следует обратить внимание на то, что ограничение ширины прямолинейных коридоров занимаемых аппроксимирующими отрезками приводит и к соответственному "обрыву" этих отрезков (на поперечных границах коридора). В результате контурная линия, которая без поперечных ограничений могла быть представлена одним отрезком, будет представлена несколькими (см., например, отрезки 4, 15 на рис.13).

Вероятно, разрешить проблемы продольной фиксации аппроксимирующих отрезков могло бы использование таких кривых (в качестве эталонов простейших отрезков), кривизна которых возрастает к их концам и минимальна в центре (например, кривых эллиптического типа). По-видимому, аппроксимация такого типа способна дать объективное (в нашем интуитивном понимании) разбиение контурных границ на участки минимальной кривизны, но этот вопрос требует дальнейших исследований.

Целесообразность продолжения исследований в этом направлении в целом очевидна. В частности, четкая продольная фиксация аппроксимирующих отрезков существенно облегчила бы решение последующей задачи целостного распознавания - сопоставления,- чем четче такая фиксация, тем, очевидно, меньше потребуется окончательных "сверок" эталонов искомых объектов с анализируемыми картинами.

Вместе с тем представляют интерес исследования, в основе которых лежала бы "передача" функции окончательной фиксации аппроксимирующих отрезков непосредственно на этап целостного распознавания контурных объектов. Причин для такой постановки задачи несколько.

Во-первых, несмотря на определенные успехи достигнутые при решении задачи продольной фиксации, четкого решения, как уже отмечалось, все же получить не удалось. Непосредственное подтверждение этому демонстрируют приведенные примеры с боковыми сторонами утюга и пяткой стельки. Конечно можно считать, что эти примеры относятся к некоторому вырожденному случаю - "слишком" плавных, протяженных и искривленных контуров. Тем не менее в приведенных примерах демонстрируется принципиальная зыбкость грани, позволяющей четко отличать случай, когда контур должен представлятся целостной дугой, а когда - составной, а именно, как аппроксимирующие отрезки должны в "истинном" случае располагаться на контуре. В зависимости от начальных приближений, случайных помех, а также "неидеальности" формы самих объектов можно получать различные представления - разбиения - контурных линий, отвечающих тождественным элементам наблюдаемых объектов.

Эта ситуация усугубляется и тем, что на практике четкое выделение контурных границ встречается сравнительно редко. Как правило, контурные линии реальных изображений представляют собой обрывки линий с плохой проработкой затемненных участков (или "переосвещенных"), а также в принципе отсутствующих, - по причине возможного частичного перекрытия другими объектами. Последнее обстоятельство представляет собой одну из характернейших особенностей решения задачи распознавания объектов в реальных условиях. В этих условиях аппроксимирующие отрезки могут не фиксироваться на "оптимальных" местах контурных границ по причине полного или частичного отсутствия последних.

Все эти обстоятельства заставляют сделать вывод о необходимости построения процедур распознавания - сопоставления - в предположении возможности скольжения аппроксимирующих отрезков по контурным границам искомых объектов. Размышления по этому поводу в целом приводят к выводу, что отдельный отрезок "простейшей" формы (со слабо выраженными изменениями кривизны), по своей сути, четко определяет проходящий контур только в поперечном направлении. Разобраться же окончательно с продольной фиксацией ("идентификацией") зачастую можно только исходя из целостных моделей искомых контурных фигур.

Рис.18 иллюстрирует это положение для простейших случаев, в частности, - неполного выделения прямолинейных контуров (рис.18а).

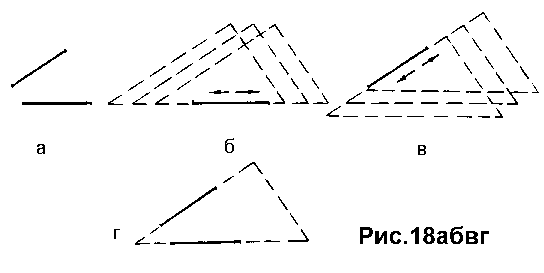
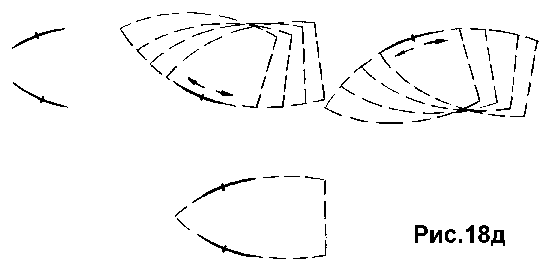
Здесь выделенные отрезки отвечают углу некоторой фигуры. Этот угол может скользить относительно каждого из выделенных отрезков (рис.18б,в), и только сочетание таких отрезков "ловит" этот угол четко (рис.18г). На рис.18д приведен аналогичный пример для "криволинейного угла" (утюга), который например фиксируется по крайней мере двумя аппроксимирующими (прилегающими) отрезками (и тем самым "определяет" эти отрезки как определенные части контура искомого объекта).

Естественно, что решение задачи целостного распознавания, при столь слабо фиксирующем - нечетком - первично-элементарном сопоставлении контуров представляет собой нетривиальную задачу. В этом случае отдельный отрезок порождает в качестве возможных все те положения искомого объекта, при которых контур его эталона только лишь совмещен с данным отрезком в поперечном направлении. Выбрать искомое положение среди столь обширного множества, порождаемого каждым отрезком наблюдаемой картины, весьма непросто.

Решению этой задачи и был посвящен следующий этап данной работы. На этом этапе был разработан метод [19], интерпретирующий задачу распознавания как "накопление гипотез" [3], который в случае объектов определенной - фиксированной - формы позволяет конструктивно решать задачу распознавания в условиях скользящего первично-элементарного сопоставления контуров.
 

Вернуться

Продолжение.