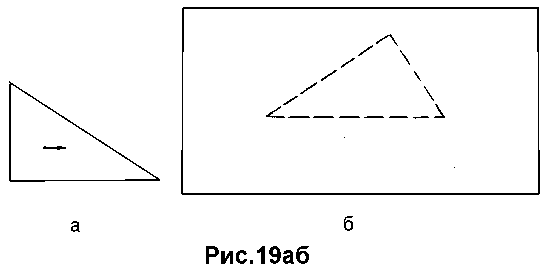
Продемонстрируем суть распознавания по принципу "накопления гипотез" на простейшем примере. Допустим, нам необходимо распознать треугольник заданной формы и размеров (рис.19а) в контексте некоторого рисунка (рис.19б).

При этом будем использовать в качестве первичных фрагментов искомой фигуры отдельные прямолинейные отрезки анализируемого рисунка, т.е. в процессе распознавания эталонный треугольник будем последовательно накладывать на анализируемый рисунок не во всевозможных положениях и ориентациях, а только в тех, когда одна из его сторон совпадает с одним из аналогичных (т.е. равных по длине) контурных отрезков этого рисунка.
Заметим, что при этом искомой фигуре на анализируемой картине будет отвечать многократное (по числу сторон) взаимоналожение эталонного треугольника (рис.19в), каждый слой которого порождается отдельным первичным фрагментом (отрезком).
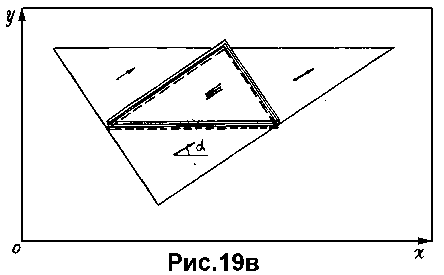
Это взаимоналожение можно регистрировать без каких-либо сравнений самих контуров. Достаточно зафиксировать в плоскости эталонного многоугольника некоторую точку, например его центр тяжести, и какой-либо луч единичной длины (т.е. базисный вектор), исходящий из этой точки и жестко связанный с данной фигурой (см. рис.19а). Теперь взаимоналожение эталонной фигуры можно регистрировать по взаимоналожению ее базисного вектора (см. рис. 19в).
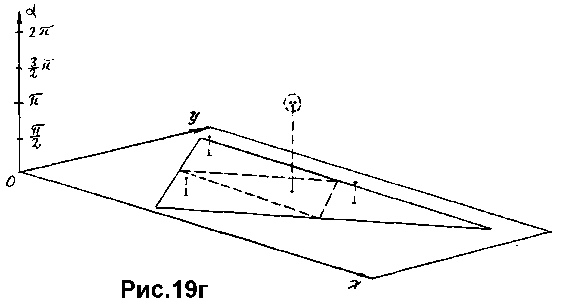
В свою очередь последняя задача сводится к поиску "максимально помеченной" точки пространства параметров, определяющих положение базисного вектора на анализируемом изображении. Каждая из этих "пометок" определяется положением базисного вектора эталонной фигуры, при одном из возможных сопоставлений ее контуров с анализируемой картиной (по отрезкам равной длины). Рис.19г иллюстрирует данную ситуацию. На этом рисунке показана аксонометрическая проекция пространства определяющих параметров (в данном случае два параметра определяют координаты начала базисного вектора, и один - угол наклона этого вектора; значения последнего параметра откладываются по вертикальной оси).
Очевидно, что такой способ распознавания (регистрация "максимально помеченной" точки) требует существенно меньших вычислительных затрат, чем непосредственная проверка на совпадение эталона искомого объекта с анализируемой картиной во всевозможных положениях, порождаемых независимо его первичными признаками (отрезками), присутствующими на этой картине.
Если на анализируемой картине исходные элементы (контурные отрезки) будут выделены не полностью, а частично (см. рис.18а), то возможным сопоставлениям эталона искомой фигуры с отдельным отрезком будет отвечать не точка, а отрезок линии, представляющий собой "след" оставленный базисным вектором в пространстве параметров, в процессе скольжения эталона относительно какого-либо выделенного отрезка (см.рис.18б,в). Искомое положение, т.е. положение, в котором стороны эталона "накрывают" наибольшее количество выделенных отрезков, отвечающих данной фигуре, очевидно, будет определяться точкой наиболее "мощного" пересечения "порожденных" отрезков в базисном пространстве.
И наконец, в случае объектов криволинейной формы, возможным сопоставлениям эталона искомой фигуры с отдельным аппроксимирующим (прилегающим) отрезком, будет отвечать некоторая кривая пространства определяющих параметров, а искомому положению - пересечение таких кривых. Конкретно, процесс распознавания в этом случае представляет собой следующую последовательность операций. На этапе "обучения" регистрируется полное неискаженное изображение искомого объекта (рис.20а). Этому изображению - эталону - приписывается некоторый единичный - базисный - вектор. Для определенности можно считать, что в качестве точки приложения выбирается центр тяжести контура эталона (хотя это и не обязательно).
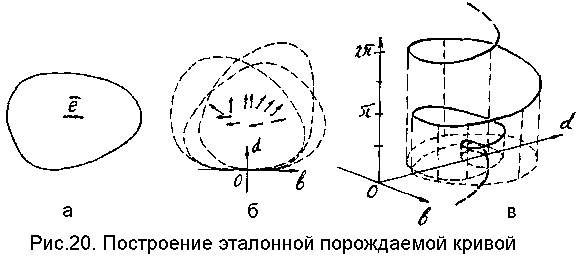
Затем, вдоль контура эталона принудительно продвигается некоторый "формальный" аппроксимирующий (прилегающий) отрезок (с непрерывной подстройкой ветвей). В процессе такого продвижения - скольжения - регистрируется положение эталона (его базисного вектора) в собственной системе координат (bOd) скользящего "формального" отрезка (рис.20б). Множество полученных наборов параметров представляет собой некоторую эталонную "порождаемую кривую". На рис.20в показана аксонометрическая проекция пространства определяющих параметров для этого случая. Здесь по вертикальной оси откладывается угол между базисным вектором и продольной осю отрезка Ob. Точки полученной кривой "показывают", какие положения может занимать эталон искомой фигуры (ее базисный вектор) относительно любого аппроксимирующего (прилегающего) отрезка лежащего на его контуре.
В процессе собственно распознавания эталонная "порождаемая кривая" последовательно сопоставляется с каждым отрезком выделенным на анализируемом изображении. Такое сопоставление представляет собой совмещение системы координат эталонной кривой с системой координат отрезка и последующий перевод ее точек в систему координат пространства параметров, определяющих положение базисного вектора на анализируемом изображении (при этом следует учитывать, что к величинам углов добавляется величина наклона текущего отрезка). Теперь точки каждой "порожденной кривой" показывают, какие положения может занимать эталон искомого объекта (его базисный вектор) относительно данного выделенного отрезка при скольжении эталона своим контуром по этому отрезку.
Таким образом, задача обнаружения плоских объектов сводится к поиску пересечений подобных кривых, отвечающих отдельным аппроксимирующим отрезкам. На рис.21 показан пример для двух отрезков (здесь xOy - система координат изображения, а по вертикальной оси откладывается угол между базисным вектором и горизонтальной осью Ox).
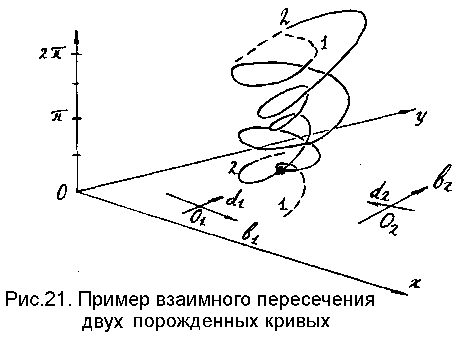
Точка пересечения большинства "порожденных кривых" определяет такое положение эталона искомого объекта (его базисного вектора), при котором контур эталона одновременно совпадает с наибольшим числом выделенных отрезков, что, очевидно, и является решением рассматриваемой задачи распознавания.
Следует отметить, что рассматриваемый алгоритм не предполагает обязательной непрерывной гладкости контурных границ искомых объектов. Для работоспособности алгоритма необходимо, чтобы число особых точек этих границ (углов) было конечным, т. е. объекты не должны напоминать "ежа" или "облако". Требуется только наличие отдельных гладких участков, что, как правило, обеспечивается самой технологией операций по формированию объектов: резанием, строганием, точением, протягиванием, ковкой и т.п., а также самой "физикой природы": силами инерции, поверхностного натяжения; закономерностями процессов скалывания, растрескивания и т.д. и т.п. Эталонная кривая строится по таким гладким участкам и представляет собой в этом случае совокупность отдельных кривых (пространства искомых параметров), отвечающих этим участкам.
Также очевидно, что отсутствие на анализируемом изображении отдельных частей контурных границ, отвечающих искомому объекту, не оказывает фатального влияния на результат распознавания, - в этом случае только соответственно уменьшится мощность искомого кластера.
Для того, чтобы сопоставить предлагаемую процедуру распознавания с уже имеющимися разработками, показать ее место среди них, а также предложить возможные расширения области применения, дадим формальную постановку задачи распознавания по принципу "накопления гипотез".
3.1. Формальная постановка задачи
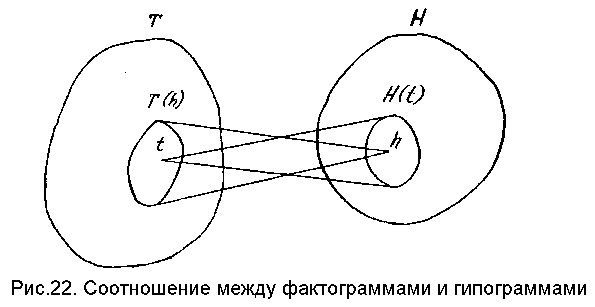
Пусть имеется множество гипотез H о некотором физическом явлении и множество фактов T, которые могут быть зарегистрированы при исследовании этого явления. При этом известно, что каждая гипотеза h <- H подтверждается определенным подмножеством фактов T(h) <= T. В дальнейшем каждое такое подмножество будем называть фактограммой данной гипотезы.
Обычно задача выбора гипотезы h_0 <- H, соответствующей некоторой совокупности фактов T_0 <= T, далее называемой множеством реализовавшихся фактов, ставится и решается как задача поиска гипотезы, фактограмма которой имеет максимальное сходство с этим множеством:
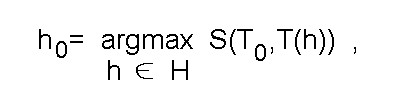
где S - функция, определяющая сходство между совокупностями фактов.
В простейшем случае сходство определяется числом элементов, одновременно принадлежащих обеим сравниваемым совокупностям:
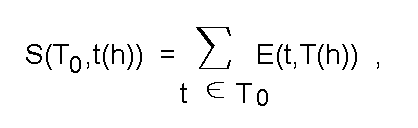
где
E(t,T(h)) = 1, если t <- T(h);
/ = 0, если t <-! T(h).
Можно сказать, что в данном случае производится поиск гипотезы, ПОДТВЕРЖДАЕМОЙ максимальным количеством реализовавшихся фактов.
Теперь заметим, что ту же задачу поиска гипотезы, соответствующей реализовавшимся фактам, можно ставить как задачу поиска гипотезы, ПОРОЖДАЕМОЙ одновременно наибольшим количеством этих фактов:
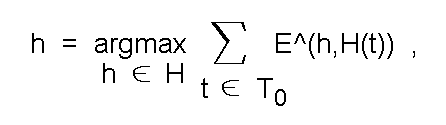
где H(t) = { h|h <- H, t <- T(h) } - подмножество гипотез, порождаемых отдельным фактом, т.е. подтверждаемых этим фактом; далее каждое такое подмножество будет называться гипограммой конкретного факта (рис.22 образно иллюстрирует суть введенных понятий);
E^(h,T(t)) = 1, если h <- H(t);
/ = 0, если h <-! H(t).
Именно этот смысл вкладывается в понятие поиска по принципу накопления гипотез [3].
Принятое наименование оправдано тем, что такая постановка задачи поиска естественным образом приводит к его реализации, основанной на использовании некоторого множества накопителей, изоморфного множеству перебираемых гипотез. В этом случае каждый очередной факт учитывается однократно, путем пометки накопителей, которые отвечают гипотезам, входящим в гипограмму, порождаемую этим фактом. После окончания перебора всех фактов и пометки накопителей остается зарегистрировать накопитель, имеющий максимальное число меток.
Первый вид поиска условно можно назвать поиском по принципу непосредственной проверки подтвержденности гипотез, а второй - по принципу косвенной проверки путем накопления порождаемых гипотез. Сравнивая эти виды поиска, прежде всего следует сказать, что получаемые с их помощью результаты принципиально эквивалентны; что объясняется тем, что количество подтверждений какой-либо гипотезы очевидно равно числу ее порождений.
Рациональность использования того или иного способа поиска гипотезы, соответствующей реализовавшимся фактам, зависит, прежде всего, от способа определения множества гипотез H, подлежащих проверке. Преимущества методики накопления гипотез оказываются бесспорными, когда гипотезы выдвигаются непосредственно по отдельным фактам, по которым производится и проверка этих гипотез, а именно, когда множество гипотез определяется как:
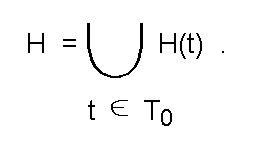
В этом случае отсутствует повторный возврат к уже просмотренным фактам, выражающийся в вычислении функции сходства.
Если же характер задачи позволяет каким-либо образом ограничить число гипотез по сравнению с тем, которое порождается всеми реализовавшимися фактами в отдельности (что довольно часто имеет место), то затраты на конструирование накопителя могут оказаться неоправданными; в этом случае можно ограничиться непосредственной проверкой подтверждения фактограм, отвечающих имеющимся гипотезам. Необходимо учитывать конкретные особенности решаемой задачи.
3.2. Методика накопления гипотез в задаче распознавания объектов
При решении задачи распознавания объектов по их изображениям в качестве фактов выступают отдельные элементы этих изображений, которые, по предположению, соответствуют некоторым элементам (фрагментам) искомых объектов. В дальнейшем такие элементы также будем называть первичными признаками. Каждый первичный признак, выделенный на анализируемой картине, порождает множество гипотез о параметрах искомого объекта, т.е. гипограмму. При этом каждой гипотезе отвечает точка пространства параметров, определяющих положение и ориентацию объекта, а отдельной гипограмме - определенное множество таких точек. Далее для простоты эти множества точек также будут называться гипограммами. Искомое положение объекта определяется точкой пересечения гипограмм. Естественно, в общем случае следует говорить об этой точке как о точке сгущения (кластеризации), т.е. о точке, в окрестность которой попадает наибольшее число гипограмм.
В последнее время алгоритмы распознавания, основанные на кластерном анализе пространства искомых параметров, привлекают всевозрастающее внимание специалистов по зрительному распознаванию объектов. Большинство исследований этого направления восходит к широко известным преобразованиям Хока [7, 20 - 27]. Существенный недостаток этих алгоритмов заключается в том, что искомые параметры рассматриваются как параметры некоторых абстрактных преобразований, переводящих элементы эталонного изображения в аналогичные элементы анализируемого изображения [22, 25]. Такая постановка задачи затрудняет понимание логики построения и дальнейшее усовершенствование подобных алгоритмов распознавания. В частности, это приводит к довольно отвлеченным рассуждениям о "коллинеарности" контурных точек [7, 28] или о "неточечных преобразованиях" [21, 22], Приходится доказывать эквивалентность результатов, получаемых с помощью этих алгоритмов и алгоритмов распознавания, в основе которых лежит сравнение с эталоном [29].
Содержательный подход к задаче распознавания как задаче поиска "взаимоналожения" модельных изображений искомых объектов, порождаемых независимо отдельными фрагментами (признаками) этих объектов [19], непосредственно подсказывает технику параметризации. Очевидно, в качестве искомых параметров следует использовать параметры простейших конфигураций структурных элементов, жестко связанных с эталоном искомого объекта и позволяющих полностью определить его положение и ориентацию. При этом суть задачи распознавания сводится к поиску взаимоналожения таких конфигураций. В случае плоских объектов базисной конфигурацией является любой единичный вектор, приписанный вначале эталону объекта (если меняется масштаб, то этому вектору можно приписать соответствующее изменение длины). В случае объемных тел базисной структурой могут быть два единичных вектора, исходящих из одной точки. Положение такой конструкции определяется шестью параметрами: три задают координаты точки приложения, два - ориентацию главного вектора этой конструкции, и один - "вращение" вспомогательного вектора вокруг главного. Можно использовать и углы Эйлера; в этом случае базисная конструкция будет представлять собой тройку взаимно перпендикулярных векторов, исходящих из одной точки. Во всех этих случаях отдельная гипограмма будет определяться по совокупности положений базисной структуры, которые она может занимать относительно данного первичного признака (фрагмента) искомого объекта.
Предлагаемая онтологическая схема представляет собой обобщение и попытку более глубокого выяснения сути подобных алгоритмов. Прежде всего, эта схема непосредственно показывает эквивалентность результатов, получаемых с помощью той или иной методики распознавания объектов. Ярким примером этого является работа матричного дешифратора, которую можно рассматривать и как параллельное сравнение с эталоном (заданным на адресном регистре) и как поиск пересечения ("ячейки сгущения") гипограмм, задаваемых адресными шинами. Следует отметить, что первоначальным толчком в направлении идеи накопления гипотез послужили идеи Гузмана [30] о выдвижении глобальных гипотез на основе локальных данных, а для идеи взаимоналожения моделей - идея Уолтца о поиске непротиворечивой (совместимой) разметки контурных ребер [31].
Возможно, предложенная онтологическая схема
послужит дальнейшему продвижению в понимании сути различных видов поиска
и взаимосвязи между ними. Рассмотренный пример, где выбор гипотезы осуществляется
простым подсчетом "бинарных" голосов, отражает только простейший случай.
Цель этого примера - показать связь "накопления гипотез" со "сравнением
с эталоном", также в его простейшей форме - "бинарным" учетом подтверждающих
фактов. В общем случае функция принадлежности ("подтверждения - порождения")
может иметь и более сложный вид: принимать непрерывный спектр значений
(например, быть нечеткой), принимать отрицательные значения (отдельные
факты могут опровергать некоторые гипотезы) и т.д. и т.п.