APPENDIX
1.6.A. Estimation of the Bell-Approximation Resolution.
Let's
consider the simplest case of two parallel segments placed on distance 2*x_0
from each other. The cross-section of the considered picture is shown on
fig.5a. On this picture the position of the approximating segment axial
line is determined by parameter x. In this case

Where k - number
of points in each segment.
Extrema of such
measure are determined by zero values of its derivative:

The denominator
of resulting expression is positive at any values of entering variables.
The numerator can be transformed to the view

This equation
has five solutions, one of which is x_1 = 0, and four others :

Two solutions
which are determined by a difference of the expressions placed under sign
of exterior square root, have imaginary values at any values of entering
variables (as x_0> 0, under the initial agreement - see fig.5a). Others
two have real values, when

Simplifying this
expression, we shall obtain that at D < sqrt(3)*x_0 investigated conformity
function has three extremums: one central and two symmetric side ones.
It is easy to show, that:

It is obvious,
if D < sqrt(3)*x_0, then S"(x)|_0 > 0, i.e. the central extremum is
a local minimum of considered conformity function of and, hence, adjacent
side exremums are local maximums of this function (see fig.5b). At D >
sqrt(3)*x_0, these maximums merge in one (see fig.5c). Positions of maximums
depending on a value of parameter D are shown on fig.5d (see the formula
for an evaluation of x_2... x_5).
1.7.A. Adding to
the Problem of the Automatic Correction of the Width of the Membership Function.
As it is affirmed,
the maximum of the function of conformity that is determined by expression

is reached at
the finite value of parameter D, when the exponent in which it is raised
in numerator - g (governing the amplitude growth rate) lays in the interval
1 < g < 2.
Let's prove this
statement.
Let's consider
an approximated segment (see fig.6b) as a continuous point set. In this
case the conformity measure is determined by an integral

Here the variable
v = d is entered to avoid confusion with differential label. The behaviour
of this measure depending on width of membership functions is defined by
a derivative on D:



Equating this
expression to zero, and introducing the variable gamma = V/D, we obtain:

In a range of
interest for us (0 < gamma < oo) this function has the maximum value
2 at gamma = 0 and asymptotically comes nearer to 1 at gamma -> oo (see
fig.6d).

|
Fig.6d
|
Its decrease
monotonicity is confirmed by that its derivative everywhere is negative
in the interval 0 < gamma < oo:

A graph of the inverse
function D/V=1/gamma (g), our actual subject of interest, is represented
on fig.6c. This graph shows, what will be the width of memberships functions
(in comparison with the flowing relative width of the approximated segment)
at reaching by the considered conformity measure of its maximum value depending
on index g, governing amplitude growth rate of memberships functions.
2.2.A. Choice of
the Step of the Start Positions for the Procedure of the Contour Boundary
Representation in Terms of the Contiguous Segments.
A beforehand
value of the least radius of neighbourhoods R_min among radii of neighbourhoods
R_c of all contour segments of the treated image was estimated. The radius
of the neighbourhood is a radius of the greatest circle with the center
on the given segment, intercrossed by it and not containing points of other
segments (fig.27).

|
Fig.27
|
Parameters of
X, Y initial sets were defined by nodes of some grid on the image plane.
Density of the grid was chosen so that in any circle in radius R_min/2
one node of this grid hitted even. In the case of a square grid its step
should be less, than R_min/sqrt(2). Remaining parameters were prescribed
identical to all sets. A value of parameter B corresponding to length of
initial contiguous segments was chosen smaller than (R_min/2)*sqrt(3). This
choice is caused by the obtained theoretical estimation for a resolving power
of the suggested approximation method. Parameter D was chosen equal 0.5*B,
A - arbitrary, P1 = P2 = 0.
2.2.B. Particularities
of the Gradiet Procedure of the Local Maximum Detection of the Bell-Conformity.
During
the given work several gradient procedures of search of local extremums
have been tested. Their principal means consist in deployment of
the frame corresponding to displacement of the central point of an approximating
segment, along ridges of the conformity function. A characteristic example
- the procedure circumscribed in [34].
However, use of such universal (that is why rather bulky) procedures does
not justify itself in a situation when the preliminary count of specificity
of the variables is possible,that simplifies extremum search. Specificity
of the variables consists here in their well defined hierarchy. First of
all the angle and cross position of a contiguous segment are arranged, a
after them - parameters of branches. And only then moving in the longitudinal
direction is carried out.
Such specificity
of variables has allowed to use effectively at the second stage of experiments
the gradient procedure in which moving on all variables of eight-parametrical
conformity measure is carried out simultaneously and basically is independent.
During searching delays are possible (misses of steps on some variables)
if parameters with higher priority were not arranged yet. In final variant
the following system of priorities was used: (+, A), (P1, P2), (D), (B1,
B2, =) where - "+" and "=" designate moving in cross and longitudinal directions
accordingly. The step on any variable increases half (with the count of restriction
on maximum value - see further) if the it is executed in the same direction,
as previous, and decreases otherwise. Thus it is considered, that those variables
were arranged, the step on which became less, than 1/4 from the maximum admissible
value on the given variable.
The last values
were chosen from the most common reasons so that as a result of each step
the new approximating segment not too overstepped the bounds of old onethe.
Steps in a longitudinal direction (and on length of the branches) were limited
to value B/2, and in cross - D/2. Steps on the angle and curvature should
not oscillate ends of the segment on value bigger than D/2, i.e.  A*MAX(B1, B2)/0.7 and
A*MAX(B1, B2)/0.7 and  P * (B/0.7)/2 should not exceed D/2. In order to prevent discretization
disclosures of analysed contours, the value of parameter D was limited
from below to the value ranging 0.5 - 2.5 distances between adjacent points
of the raster. From above parameter D was limited by value B/2.
P * (B/0.7)/2 should not exceed D/2. In order to prevent discretization
disclosures of analysed contours, the value of parameter D was limited
from below to the value ranging 0.5 - 2.5 distances between adjacent points
of the raster. From above parameter D was limited by value B/2.
Particularly
such restrictions are organized so, that at the approach to one of them
it is authorized to make the following step only on half of the distance
before this restriction. It simply enough ensures a possibility of increase
of a step if a necessity of movement in the opposite direction exists.
Initial steps on separate components were chosen equal to the half of their
greatest possible values. Thus initial values of parameters B and D were
accepted equal 10 and 4 accordingly, and as much as the possible admissible
step value on D equal 0.5. Search procedure of the next conformity measure
maximum stopped when steps on all variables became smaller, than 0.2 of their
maximum possible admissible values.
As a rule, search
of the maximums corresponding to contour segments required on the average
60-80 steps on theof declination angle and position in the cross direction
at 8-12 steps in the longitudinal direction.
2.2.C. Estimation of quality - filling ratio of
contiguous segments.
The property
of filling ratio of a resulting segment is defined as follows:

Where
t_1, t_2... t_m
- coordinates of points of the raster;
E (t_i, h) -
|
membership function which is determined
by parameters of the found maximum
(h = {X, Y, A, D, P1, P2, B1, B2});
|
e (t_i) -
|
the indicator function marking contour
points:
= 1 if the
given raster point is included into the number of contour points;
= 0, otherwise.
|
In the first
series of experiments those segments were only considered acceptable which
have filling ratio over 0.5.
According to
sparsed representation, the filling ratio criterion of contiguous segments
was modified also. The essence of such modification consists in the following.
The axial line of a tested segment is divided into the intervals equal to
a step of tracking of contour boundaries. Within the limits of each interval
there is the contour point nearest to the axial line. Values of memberships
functions to these points are summarized, and the obtained outcome is divided
on the greatest possible value of this sum when within the limits of each
interval there is a point laying on the segment axial line. In the second
series of experiments the segments which filling ratio exceeded 0.8 were
considered as acceptable ones.
2.2.D. Additional
techniques.
To
avoid a repeated finding of segments and to simplify searching less expressed
maximums,
the contour
points laying inside the image piece corresponding the found segment, were
excluded from the further reviewing. Each of such pieces represents a corridor
in width 2D/0.7, enclosing the axial line of the given segment; length of
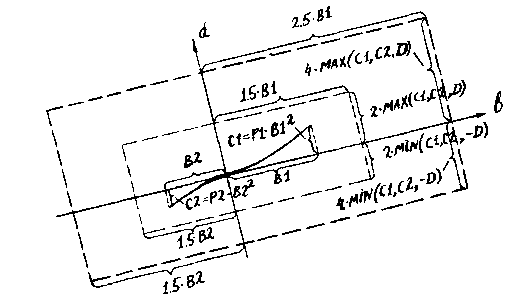
branches of this corridor - B1/0.7 and B2/0.7 (fig.9).

|
Fig.9
|
To avoid superfluous losses
of time, the operation of rough choice of the contour points concerning
to the flowing contiguous segment was applied. In the beginning for an evaluation
of coincidence measure gradient of chosen contour points (the list of references
to their initial set is formed) which lay inside a wide rectangle enclosing
the contiguous segment in its flowing position (such neighbourhood is shown
by fat primes on fig.12).
|
Fig.12
|
Further, on each step a
possibility of build-up of new, narrower neighbourhood for a flowing
position of the contiguous segment (thin primes on fig.12), not passing
out of former wide neighbourhood is checked. If it is impossible, a list
of references is made on a new wide neighbourhood.
Operations
of deletion and preliminary choice have not only engineering sense.
A solution of basic problems depends on their organization too. In particular,
ability of the procedure to understand complicated situations depends on
their organization, - at processing of false concentrations of contour
points, in the case of capture of several segments. In similar cases
the number of steps noticeably increased (sometimes so, that it was necessary
to discontinue compulsorily process of searching). Detection of such situations
was carried out by criterion of filling ratio of resulting segments by contour
points. An example of such situation is shown on fig.11. On this picture
it is shown the initial (dotted line) and finite (solid line) positions of
the contiguous segment, corresponding to process of search of one local maximum.
Apparently, the right branch of the initial contiguous segment has not had
time to be rounded along the corresponding piece of the contour line
and intersected an adjacent contour.

|
Fig.11
|
Thus it is obvious, that
deletion of the piece of image corresponding to the finite position of such
segment is wrongful. The contiguous segments started from other initial
positions can correctly interpret an observed picture. The solution accepted
in this occasion is based on this reason. The elementary contours laying
in a neighbourhood of the contour movement from which led to an unacceptable
segment, were excluded from candidates in initial approximations. So the
situation shown on fig.11, for example, was treated - as an initial approximation
the elementary segment was chosen, the distance from which up to an outside
contour exceeded the corresponding distance for the initial segment which
had led to false outcome.
This example illustrates
common logic of solution of complicated situations. To solve them
it is necessary to begin from the outside - from the "free" ends of
entering lines.
3.5.A. Some Details
of the Procedure of the Accumulation of the Hypotheses.
In the
program realizing hypotheses accumulation procedure information only about
the marked zones is stored. For this purpose some array is assigned, the
entry in which is made with help of L-hashing [35] at which zone number is a key, and
the hashing function is a remainder of division of zone number on array size.
In the carried out experiments this array consisted of 4096 cells. Thus the
initial search address of the cell corresponding to a zone with given number
(hashing function) was obtained by zeroing of top digits of this number
(since 13-th). In each cell, except for a zone key (number in a common hypothetical
three-dimensional array of the zones), a reference to a description of the
given zone is stored. The zone description too is one cell of some array
in which the bites are marked corresponding to numbers of those hypograms
which marked the given zone. Thus the zone mark with a separate hypogram
is reduced to logic addition of its descriptions to the cell in which bite
is marked that corresponds to the current hypogram number(an array of such
cells is prepared beforehand). After the termination of marking process with
all hypograms, operation of transformation of contents of each description
into number of hypograms which marked it (for each description it is one
machine command by estimation of units in the given cell) is started.
At execution
of smoothing procedure numbers of neighboring zones are not calculated anew
but d are calculated by addition to components translating the number of
the central zone into number of one of 27 adjacent zones (3x3x3). These
components are calculated beforehand. The logic of their evaluation is defined
by logic of an evaluation of common linear number of an element (zone) in
a multivariate (three-dimensional) array.
To reduce number
of contiguous segments tracing a reference contour at build-up of its hypogram,
the next reference hypogram points are under construction on a forward branch
of last contiguous segment. It is possible to tell, that on this branch
the fictitious tangential contiguous segment moves ahead, and in its frame
positions of the basis vector are registered. The boundary of such construction
is defined by mismatch of positions of the basis vector in frames of actual
and fictitious segments. Thus a movement step of actual segments is continuously
arranged with the help of feed-back so that to keep the mismatch value within
the limits of a zone quarter, and a step of fictitious segments have to
keep adjacent points of the reference hypogram within the limits of one zone.
The zone, as well as earlier, is meant as an element of subdivision of parametrical
space. If it is not possible to be made, it is accepted, that in this place
the hypogram has a rupture and its construction proceeds from other place
of the standard contour.
3.5.B. Illustration
rationality of smoothing operation.

|
Fig.26
|
The initial histogram of
the most powerful cluster (fig.24a and fig.26b) is shown on fig.26a. Here
weight of the zone is a number of hypograms marking its. Rationality of
smoothing operation in this case is confirmed by a view of the initial
histogram of the same cluster at size of zones reduced in one and a half
time (fig.26c). Thus also the centers of zones of the space of search parameters
accordingly have somewhat moved. This example shows that relatively big
weight of a collateral ejection (fig.26a) is caused, first of all, by accidents
of distribution of hypogram points within the limits of adjacent zones.
In [3] the operation of multiple smoothing
has been suggested. In this case smoothing is done{made} iterativelly until
the condition will be satisfied that at two sequential stages the same zone
(besides the unique one) has the maximum sum (among all zones at the given
stage). The center of this zone is accepted as a search cluster point. Though
such the procedure has not shown crucial advantages in comparison with once
made smoothing, it is expedient to have its in a collection of tools of the
analysis of hypogram intersection. Multiple smoothing will coordinate a
cluster point (zone) with its environment. If this point is on a cluster
boundary it is gradually shifted in its center. The stability of this point
(zone) at several sequential stages of smoothing is some performance of
its common reliability. Besides, if the cluster top is not acute, i.e. consists
of several zones that (due to the count of neighboring zones) one zone of
maximum weight will be allocated which position will depend on a context
(i.e. weightinesses of enclosing zones).
In last version
of program realization of hypotheses accumulation process an attempt has
been undertaken to limit an amount of the zones participating in the subsequent
procedure of smoothing. For this purpose so-called areas of intersection
were selected, which represent set of the zones marked more than two hypograms,
and also one time marked zones directly adjoining to this set (the neighbourhood,
as well as earlier, the nearest 3*3*3). However, in spite of the fact that,
for example in the circumscribed experiment, execution time of the smoothing
procedure on the average was reduced with 1.5 up to 0.5 s, it was additionally
required about 0.5 s for detection of these areas (thus the number of analysed
zones was reduced on the average in 5 times). Probably, this procedure will
have essential advantages at more rigid restrictions on entrance in an area
of intersection. Naturally, the operation of restriction of number of analysed
zones has an essential importance at multiply repeated smoothing.


![]()
















