где k - число точек в каждом отрезке.

Экстремумы такой меры определяются нулевыми значениями ее производной:

   

Знаменатель результирующего выражения положителен при любых значениях входящих переменных. Числитель можно преобразовать к виду

   

Это уравнение имеет пять решений, одно из которых x_1 = 0, и четыре других:

   

Два решения, которые определяются разностью выражений, стоящих под знаком внешнего квадратного корня, имеют мнимые значения при любых значениях входящих переменных (так как x_0 > 0, по начальному соглашению - см. рис.5a). Два других имеют действительные значения, когда

   

Упрощая это выражение, получим, что при D < sqrt3*x_0 исследуемая функция сходства имеет три экстремума: один центральный и два симметричных боковых. Нетрудно показать, что:

   

Очевидно, если D < sqrt(3)*x_0, то S"(x)|_0 > 0, т.е. центральный экстремум является локальным минимумом рассматриваемой функции сходства и, следовательно, соседние боковые - локальными максимумами этой функции (см. рис.5b). При D > sqrt(3)*x_0, эти максимумы сливаются в один (см. рис.5c). Положения максимумов в зависимости от значения параметра D показаны на рис.5d (см. формулу для вычисления x_2...x_5).

Как утверждается, максимум функции сходства, определяемого выражением

   

достигается при конечной величине параметра D, когда показатель степени, в которую он возводится в числителе - g (регулирующий скорость роста амплитуды) лежит в интервале 1 < g < 2.

Докажем это утверждение.

Будем рассматривать аппроксимируемый отрезок (см. рис.6b) как непрерывное множество точек. В этом случае мера сходства определяется интегралом

   

Здесь переменная v = d введена для того, чтобы избежать путаницы с обозначением дифференциала. Поведение этой меры в зависимости от ширины функции принадлежности определяется производной по D:

   

   

   

Приравнивая это выражение нулю, и вводя переменную gamma = V/D, получаем:

   

В интересующем нас диапазоне (0 < gamma < oo) эта функция имеет максимальное значение 2 при gamma= 0 и асимптотически приближается к 1 при gamma -> oo (см. рис.6d).

Рис.6d

 Монотонность ее убывания подтверждается тем, что ее производная всюду отрицательна на интервале 0 < gamma < oo:

   

График, собственно интересующей нас, обратной функции D/V=1/gamma(g), представлен на рис.6c. Этот график показывает, какой будет ширина функции принадлежности (по сравнению с текущей относительной шириной аппроксимируемого отрезка) при достижении рассматриваемой мерой сходства своего максимального значения в зависимости от показателя g, регулирующего скорость роста амплитуды функции принадлежности.

Рис.27

Параметры X,Y начальных наборов определялись узлами некоторой сетки на плоскости изображения. Ее густота выбиралась так, чтобы в любую окружность радиусом R_min/2 попадал хотя бы один узел этой сетки. В случае квадратной сетки ее шаг должен быть меньше, чем R_min/sqrt(2). Остальные параметры устанавливались одинаковыми для всех наборов. Величина параметра B, отвечающего длине начальных прилегающих отрезков, выбиралась меньшей, чем (R_min/2)*sqrt(3). Этот выбор обусловлен полученной теоретической оценкой для разрешающей способности предлагаемого метода аппроксимации. Параметр D выбирался равным 0.5*B, A - произвольным, P1 = P2 = 0.

Такая специфика переменных позволила на втором этапе экспериментов эффективно использовать градиентную процедуру, в которой движение по всем переменным восьмипараметрической меры сходства осуществляется одновременно и в принципе независимо. В процессе поиска возможны задержки (пропуски шагов по некоторым переменным), если параметры с более высоким приоритетом еще не подстроились. В окончательном варианте использовалась следующая система приоритетов: (+,A), (P1,P2), (D), (B1,B2,=), где - "+" и "=" обозначают движения в поперечном и продольном направлениях соответственно. Шаг по какой-либо переменной увеличивается наполовину (с учетом ограничения на максимальную величину - см. далее), если он исполняется в том же направлении, что и предыдущий, и уменьшается в противном случае. При этом считается, что подстроились те переменные, шаг по которым стал меньше, чем 1/4 от величины максимально допустимого по данной переменной.

Последние величины выбирались из самых общих соображений так, чтобы в результате каждого шага новый аппроксимирующий отрезок не слишком выходил за границы старого. Шаги в продольном направлении (и по длине ветвей) ограничивались величиной B/2, а в поперечном - D/2. Шаги по углу и кривизне не должны были колебать концы отрезка на величину большую чем D/2, т.е.  A*MAX(B1,B2)/0.7 и  P*(B/0.7)/2 не должны превышать D/2. Во избежание проявлений дискретности задания анализируемых контуров величина параметра D ограничивалась снизу величиной, изменяющейся в диапазоне 0.5 - 2.5 расстояний между соседними точками растра. Сверху параметр D ограничивался величиной B/2.

Конкретно такие ограничения организованы так, что при подходе к одному из них следующий шаг разрешается делать только на половину расстояния до этого ограничения. Этим достаточно просто обеспечивается возможность увеличения шага при необходимости продвижения в обратном направлении. Начальные шаги по отдельным компонентам выбирались равными половине их максимально возможных величин. При этом начальные значения параметров B и D принимались равными 10 и 4 соответственно, а максимально допустимая величина шага по D равной 0.5. Процедура поиска очередного максимума меры сходства останавливалась, когда шаги по всем переменным становились меньшими, чем 0.2 их максимально допустимых величин.

Как правило, поиск максимумов, отвечающих контурным отрезкам, требовал в среднем 60 - 80 шагов по углу наклона и положению в поперечном направлении при 8 - 12 шагах в продольном направлении.

Заполненность результирующего отрезка определяется следующим образом:

   

где

t_1, t_2 ... t_m - координаты точек сетчатки (растра);

E(t_i,h) -	функция принадлежности, которая определяется параметрами найденного максимума  (h = {X,Y,A,D,P1,P2,B1,B2});
e(t_i)   -	индикаторная функция, отмечающая контурные точки: = 1, если данная точка сетчатки входит в число контурных точек; = 0, в противном случае.

В первой серии экспериментов считались приемлемыми только те отрезки, заполненность которых превышала 0.5.

В соответствии с прореженным представлением был модифицирован и критерий заполненности прилегающих отрезков. Суть такой модификации состоит в следующем. Осевая линия проверяемого отрезка разбивается на интервалы, равные шагу отслеживания контурных границ. В пределах каждого интервала находится контурная точка, ближайшая к осевой линии. Значения функции принадлежности в этих точках суммируются, и полученный результат делится на максимально возможную величину этой суммы, когда в пределах каждого интервала имеется точка, лежащая на осевой линии отрезка. Во второй серии экспериментов приемлемыми считались отрезки, заполненность которых превышала 0.8.

Рис.9

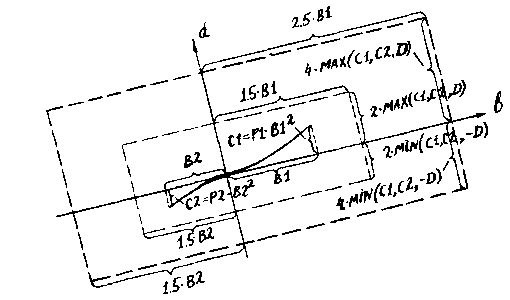
Для того чтобы избежать лишних потерь времени, применялась операция грубого выбора контурных точек, относящихся к текущему прилегающему отрезку. Вначале для вычисления градиента меры сходства выбираются контурные точки (формируется список ссылок на исходное их множество), которые лежат внутри широкого прямоугольника, окружающего прилегающий отрезок в его текущей позиции (такая окрестность показана жирными штрихами на рис.12).

Рис.12

Далее, на каждом шаге проверяется возможность построения новой, более узкой окрестности для текущего положения прилегающего отрезка (тонкие штрихи на рис.12), не выходящей за пределы прежней, широкой окрестности. Если это невозможно, список ссылок составляется по новой широкой окрестности.

Операции вычеркивания и предварительного выбора имеют не только технический смысл. От их организации зависит решение и принципиальных проблем. В частности, от их организации зависит способность процедуры разбираться в сложных ситуациях, - при обработке ложных скоплений контурных точек, в случаях захвата нескольких отрезков. В подобных случаях число шагов заметно возрастало (иногда настолько, что приходилось принудительно останавливать процесс поиска). Выявление таких ситуаций осуществлялось по критерию заполненности результирующих отрезков контурными точками. Пример такой ситуации показан на рис.11. На этом рисунке показано начальное (пунктиром) и конечное (сплошной линией) положения прилегающего отрезка, отвечающие процессу поиска одного локального максимума. Как видно, правая ветвь начального прилегающего отрезка не успела закруглиться вдоль соответствующего участка контурной линии и перерезала соседний контур.

Рис.11

При этом очевидно, что вычеркивание участка изображения, отвечающего конечному положению такого отрезка, неправомерно. Прилегающие отрезки, запущенные из других начальных положений, могут правильно интерпретировать наблюдаемую картину. Принятое по этому поводу решение основано именно на этом соображении. Элементарные контуры, лежащие в окрестности контура, движение от которого привело к неприемлемому отрезку, исключались из кандидатов в начальные приближения. Так, например, обрабатывалась ситуация, показанная на рис.11, - в качестве начального приближения выбирался элементарный отрезок, расстояние от которого до постороннего контура превышало соответствующее расстояние для начального отрезка, приведшего к ложному результату.

Этот пример иллюстрирует общую логику разборки сложных ситуаций. Разбирать их надо начинать извне - от "свободных" концов входящих линий.

При выполнении процедуры сглаживания номера окрестных зон не вычисляются заново, а вычисляются путем сложения с добавками, переводящими номер центральной зоны в номер одной из 27 соседних зон (3х3х3). Эти добавки вычисляются заранее. Логика их вычисления определяется логикой вычисления общего линейного номера элемента (зоны) в многомерном (трехмерном) массиве.

Для того чтобы уменьшить число прилегающих отрезков, отслеживающих эталонный контур при построении его гипограммы, очередные точки эталонной гипограммы строятся по передней ветви последнего прилегающего отрезка. Можно сказать, что по этой ветви продвигается фиктивный касательный прилегающий отрезок, и в его системе координат регистрируются положения базисного вектора. Граница такого построения определяется рассогласованием положений базисного вектора в системах координат фактического и фиктивного отрезков. При этом шаг продвижения фактических отрезков непрерывно подстраивается с помощью обратной связи так, чтобы удержать величину рассогласования в пределах четверти зоны, а шаг фиктивных - чтобы удержать соседние точки эталонной гипограммы в пределах одной зоны. Под зоной, как и ранее, подразумевается элемент разбиения параметрического пространства. Если этого сделать не удается, то принимается, что в этом месте гипограмма имеет разрыв и ее построение продолжается с другого места контура эталона.

Рис.26

Начальная гистограмма наиболее мощного сгущения (рис.24a и рис.26b) показана на рис.26a. Здесь вес зоны - это число пометивших ее гипограмм. Рациональность операции сглаживания в данном случае подтверждается видом начальной гистограммы того же сгущения при размере зон, уменьшенном в полтора раза (рис. 26c). При этом соответственно несколько сдвинулись и центры зон пространства искомых параметров. Этот пример показывает, что относительно большой вес побочного выброса (рис.26a), обусловлен, в первую очередь, случайностями распределения точек гипограмм в пределах соседних зон.

В [3] была предложена операция многократного сглаживания. В этом случае сглаживание делается итеративно до тех пор, пока не будет удовлетворено условие, что на двух последовательных этапах одна и та же зона (притом единственная) имеет максимальную сумму (среди всех зон на данном этапе). Центр этой зоны принимается в качестве искомой точки сгущения. Хотя такая процедура не продемонстрировала решающих преимуществ по сравнению с однократным сглаживанием, представляется целесообразным иметь ее в наборе средств анализа картины пересечения гипограмм. Многократное сглаживание согласует точку (зону) сгущения с ее окружением. Если эта точка находится на границе сгущения, то постепенно она сдвигается в его центр. Устойчивость этой точки (зоны) на нескольких последовательных этапах сглаживания является некоторой характеристикой ее общей надежности. Кроме того, если вершина сгущения не острая, т.е. в нее входит несколько зон, то (за счет учета окрестных зон) выделится одна зона максимального веса, положение которой будет зависеть от контекста (т.е. весомости окружающих зон).

В последней версии программной реализации процесса накопления гипотез была предпринята попытка ограничить количество зон, участвующих в последующей процедуре сглаживания. Для этого выделялись так называемые районы пересечения, которые представляют собой совокупность зон, помеченных более чем двумя гипограммами, а также однократно помеченные зоны, непосредственно примыкающие к этой совокупности (соседство, как и ранее, ближайшее 3х3х3). Однако, несмотря на то, что, например, в описанном эксперименте время выполнения процедуры сглаживания в среднем сокращалось с 1.5 до 0.5 с, требовалось дополнительно около 0.5 с для выделения этих районов (при этом число анализируемых зон сокращалось в среднем в 5 раз). Возможно, эта процедура будет иметь существенные преимущества при более жестких ограничениях на вхождение в район пересечения. Естественно, что операция ограничения числа анализируемых зон имеет существенное значение при многократно повторенном сглаживании.