| Russian |

|
| Fig.I |
The gradual divergation
is the basic moment which is necessary for including in model
of approximating shapes. The function estimating a membership of points
to a individual segment should have a maxima on centre of a segment, and
gradually reduce the value on its periphery. The provisional view of such function
is shown on fig.7. Here parameter B corresponds a half-length of
an approximating segment, is similar to, how parameter D - to a half-width.

|
| Fig.7 |
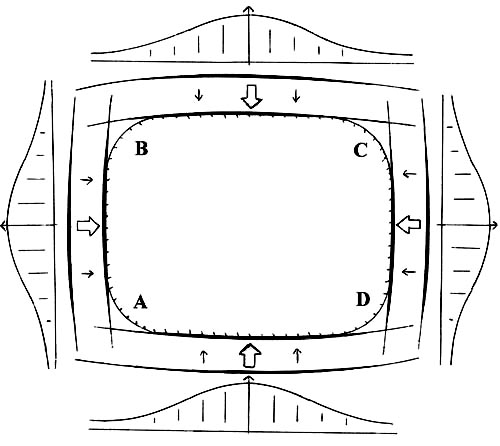
On fig.I the linear images defined by the given concept are schematic shown. The diminution of their width (them thinning) responds to diminution of their geometrical determinancy - to clearness. Appropriate shapes of bell-shaped function of a membership are figured from an exterior side of each segment.
It is visually possible
to represent, that approximating is carried out with certain arcs - small
arcs with “thinning” to its ends (the association and with typographical
round brackets is also pertinent). Such segments - small arcs
are named by contiguous segments because their branches, in common,
only adjoin to approximated lines. Their other semantic title - segments
with the fuzzy ends.
To concept of contiguous segments - segments with the fuzzy ends it
is possible to approach and on the other hand, - not from a diminution of
their determinancy on periphery, but, on the contrary, - its magnifications
to centre. Magnification of a geometrical determinancy to centre - the
middle, with adjoin of branches, is just that ensures a maxima of
determinancy in definition of the tangential direction. Here, abstract
- differential feature - a direction of a line in a point (the first derivative),
obtains, in face of contiguous segments, the stable foundation for the
definition in actual conditions. There is a potential possibility of wider
practical usage of this feature at the analysis of actual data.
These reasons
also have underlain a suggested method of the description of contour
boundaries in terms of segments with fuzzy ends. In the carried out researches
as axial lines of approximating segments curves of the simplest analytical
type, namely - the central pieces of parabolas were used. And each branch
could have own curvature. For fine length tuning of branches the mechanism
similar to fine tuning of width of segments was used. The conformity measure
builted according to these reasons, has the following mathematical expression:

Where
| b_i, d_i - |
the parameters defining a position of
a contour point in own frame of an approximating segment (fig.8); these
parameters are defined on coordinates of the point x_i, y_i with
the help of transformations |
| b_i = (x_i
- X)*cos(A) + (y_i - Y)*sin(A), |
|
| d_i = - (x_i - X)*sin(A)
+ (y_i - Y)*cos(A); |

|
| Fig.8 |
| X,Y - |
coordinates of the center of the segment; |
| A - |
the angle of declination of the segment;
|
| P = |
P1, if b_i >= 0 (curvature
of the right branch), P2, if b_i < 0 (curvature of the left branch); |
| B = |
B1, if b_i >= 0 (length
of the right branch), B2, if b_i < 0 (length of the left branch); |
| D - |
a half-width of the membership function.
|
A separate approximating
segment defined by such measure of conformity is symbolically shown
on fig.8. Here decrease of thickness of the segment reflects decrease
of its clearness, i.e. degrees of correspondence to an approximated contour.
The contour image on which basic serviceability
of this procedure was checked is shown on fig.10a.

|
| Fig.10a |
The size of an initial half-tone picture
is equal - 290x196 points. For detection of contour boundaries the known
Hueckel's operator [5.6] was used. In total,
800 contour points were chosen approximately. Initial positions of contiguous
segments were defined by nodes of a regular grid with 12 raster points step
(reasons on the basis of which this step was set, are stated in Appendix_2.2.A.). Values of remaining
parameters were accepted as the following: B1 = B2 = 5, D = 2.5, A = 0,
P1 = P2 = 0.
Initial approximations had the most
various positions concerning approximated pieces. Nevertheless, in supressing
majority, from 384 starts having here a place, procedure of gradient "fine
tuning" founded the maximum of the bell-conformity measure defining
an actual contiguous segment (fig.10b).

|
| Fig.10b |
The experiments carried out in this
way have shown that the maximums corresponding to the segments in search
have pure slopes. Really, on these slopes there are no ejections
(they are swallowed by the basic extremums) in which gradient procedure
could "lose the way". These experiments have proved a basic possibility
of deriving of the description of contour figures in terms of contiguous
(tangents) of the segments corresponding to our intuitive representations.
At the same time, the analysis of behaviour
of the gradient procedure originally used for search of local maximums
of a bell-conformity measure [2], has shown, that in neighbourhoods of the
maximums (i.e. at the final stages of search) the conformity function
looks like the long, narrow ridges prolated along axial lines of contour
boundaries. Thus, approximating segments can long oscillate in the cross
direction to these lines, with very slow movement in the longitudinal direction.
For fast transition of these ridges in [3] it was offered to displace during
search the central point of an approximating segment not on axes of the
image coordinate system but along and cross of flowing direction of its
axial line. As the axial line of an approximating segment is gradually arranged
under the axial line of the represantation piece of contour boundary, longitudinal
moving of the segment is carried out directly along the axial line of the
mentioned ridges. Such organization of the search procedure of local maximums
of the conformity measure enabled rather fast and legiblly to pass the above
mentioned ridges of this measure. More in detail about the choice of value
of steps it is said in Appendix_2.2.B.
Further. As initial approximations in
the subsequent experiments, the most legible elements of contour boundaries
selected by the Hueckel's operator were accepted. Besides, sparsed
representation of contour boundaries was used. As contour points the central
points of contour-boundary (edge) patterns of the Hueckel's operator
were assumed, instead of all raster points placed under them as it was
in the first series of experiments were accepted.
According to sparsed representation,
the criterion of filling ratio of contiguous segments [Appendix 2.2.C] was modified also.
A contour image on which serviceability
of the advanced procedure of representation of contour boundaries was
checked by contiguous segments is shown on fig.13. A size of the initial
half-tone picture - 216x216. In this case, diameter of the entering piece
of the Hueckel's operator was equal to seven (7) points of the raster. Overlapping
at tracking of the contours was equal to a half of diameter of this piece.
Hence, a step between "sparsed" contour points was 3.5. Contours of the exibited
image contain 215 points.

|
| Fig.13 |
On the same picture the outcomes of work
of new procedure (resulting contiguous segments) are shown.
The proposed organization of the procedure
of gradient searching, sparsing of contour points and choice of the initial
approximations defined on the best pieces of contour boundaries enabled
to increase essentially stability of the process of the description of
these boundaries in terms of contiguous segments. Necessary accounting
time was sharply reduced also. Representation of a contour picture (fig.13)
with contiguous segments has demanded 50 sec of computation time, and a
picture of the same order of the complexity shown on fig.10 (the first
series of experiments [2]), with the
help of initial variant of this procedure - over 20 minutes.
The carried out experiments confirmed
a possibility of practical realization of the concept of contiguous segments
- segments with fuzzy ends.
In Appendix_2.2.D
the some tactical problems of the organization of the search process
of local maximums of the bell-conformity measure are considered.
Further researches
on size optimization of steps of gradient procedure seems to be expedient.
In the considered variant the choice of their value was carried out on
the base of the most common reasons.
Now for detection
of false situations (in particular, at capture of several
segments),the final, rather bulky property criterion of filling ratio
of contiguous segments is used only. For more operative estimation of
the situations arising during the bell-approximation process, a use of the
information on behaviour of the gradient procedure - character and
number of steps - is possible. For the same purposes it is possible to
use a mutual coherence (confirmation) of the approximating segments related
to the same piece of contour boundaries. There is that natural reason,
that if one contiguous segment confirms by its branch the cross position
and orientation of the central piece of other segment (and vice versa),
then, most likely, there is the set of contour points under these approximating
segments corresponding to our concept about an uniform line segment.
The applied mode
of preliminary choice of contour points is deintended for work in the conditions
of full absence of information on topological connections between individual
elementary contours. However, as an operational experience shows for actual
images, contour boundaries are traced through the help of local operators
on rather extended pieces. In this connection treatment of the connected
pieces of contour boundaries instead of acnodes from some area is prospective.
By the way, it can facilitate approximation of close placed contours too.
Use of the Hueckel's
operator for search of contour boundaries of analysed images is caused
by a necessity of simplification of experiments. Most likely, the suggested
approximation method will be efficient at use of more simple operators
too, for example at the use of the simplified Hueckel's operator [18], the Sobel's operator and possibly of the
Roberts simplest operator [7]. Besides, a possibility
is supposed to build-up of an operator of similar outcomes quality (and
of operation principle) to the Hueckel's operator, but more fast-acting.
The basic share
of computation time in the procedure of detection of contiguous segments
is expended on a sequential evaluation of contributions of contour points
in a flowing value of the coincidence measure gradient. The operating
time of procedure can be reduced essentially if to calculate these contributions
in the parallel way using a specialized computer.
All evaluations
were carried out in format of numbers with floating point. There are
no principal difficulties in their transformation into integer form. Thus
byte (or slightly greater) representations would be enough in most cases.
Obvious replacement of direct analytical evaluations by the table representation
of bell-like (one-dimensional) functions and their derivatives here will
allow to reduce sharply calculation time. Necessary for its products can
also be determined employing tables. Though the volume of such tables
is great, but it does not exceed engineering possibilities of used computing
tools (for storage of these tables memory about several tens kilobyte
is required).
As a whole, the increase of operational
speed of the representation procedure of contour boundaries by contiguous
segments on several orders is quite real.
In this connection
an experimental examination of serviceability of the representation
procedure of contour boundaries by contiguous segments has revealed the
following problem. As appeared, parabolic contiguous segments tend to
run into smooth inflections of contour boundaries. The example of representation
of contour boundaries when movement of approximating segments in a longitudinal
direction is carried out in a direction of corresponding component of conformity
measure gradient is shown on fig.14.

|
| Fig.14 |
And such arrival
is caused not by width of memberships functions as it was in the case of
root-mean-square approximation of contour boundaries by rectilinear segments.
In order to prevent a possible disclosure of structure delicacies
of the conformity function caused by sparsing of contour boundaries, the
minimum width of memberships functions was limited to a size approximately
equal to a step between sparsed contour points (D = 1.5). Experiments have
shown noncriticality of the obtained outcomes to a choice of this size (trial
experiments were carried out at D_min = 0.5 - 2.5).
The analysis
of this situation has allowed to draw a conclusion that arrival
here is defined by the form of approximating curves. Curvature of parabolas
is maximum in the center and decreases to the periphery, therefore parabolas
are easily entered in such pieces of contour boundaries.
In work [3] for restriction of the running tendency
of parabolas it was offered to move aside branches of smaller curvature.
However, as appeared, thus counteraction is required to slipping
of contiguous segments to the ends of representation pieces at fuzzy expressed
linearity maximums (fig.15). To solve this problem correctly
was not possible, - it was not possible to select univalently any strategy
of switching of longitudinal moving force which would enable to avoid
simultaneously slipping of approximating segments and arrivals
on smooth inflections.

|
| Fig.15 |
In last version
of the procedure of approximation with contiguous segments a soft
restriction of width of rectilinear corridors, which these segments can
occupy, was suggested. Mathematically, such restriction expresses that
at an evaluation of individual components of a gradient of the conformity
measure the contour points are taken into account with weight computed
under the formula

Where
| d_i - |
deviation of a contour point from a
straight line tangenting the contiguous segment in its central point,
i.e. from the longitudinal axis of its own frame; |
| U - | a half-width of a rectilinear corridor occupied by the segment (fig.16). |

|
| Fig.16 |
The second series
of the experiments described in the previous section (their outcomes
are shown on fig.13) carried out with the similar count of contour points,
i.e. contributions of these points to values of components of the conformity
measure gradient were multiplied on their weights with the count of width
of an admissible corridor. Thus for an evaluation of the component corresponding
to longitudinal movement, the corridor with a half-width equal 2.5, and
for all remaining components - a corridor with a half-width equal 5 was
used.
Smooth (gradual)
restriction of width of the rectilinear corridors occupied by contiguous
segments, has allowed to avoid their explicit arrivals on smooth
inflections and slipping to the ends of represantation pieces.
At the same time,
here again a legible solution of the problem of longitudinal fixing of
approximating segments to obtain it was not possible. At use of boundaring
rectilinear corridors the separate approximating segment can lose sensitivity
ends of a represented contour line. It can happen, if this line has a sufficient
expansion and curvature and consequently can leave for longitudinal boundaries
of the boundaring corridor. To increase width of the corridor it is impossible,
- the tendency of a parabola to run into smooth inflections begins to affect.
An example of such contour lines are contour boundaries of insoles corresponding
to its heel (fig.13), and also to lateral faces of an iron when contours
of this object are submitted full enough (fig.17).

|
| Fig.17 |
In similar cases
the approximating segments should be fixed arbitrarily-compulsorily.
The mechanism of such fixing consisted in that longitudinal movement
of the approximating segment in one direction was authorized only on half
of the distance between two points in which there was a change of movement
direction (in the beginning this distance was set equal to a diagonal
of the analysed image).
It is necessary
to pay attention that width restriction of the rectilinear corridors
occupied by approximating segments leads also to respective breakage
of these segments (on cross corridorboundaries). In outcome the contour
line which without cross restrictions could be submitted by one segment,
will be submitted by several ones (see, for example, segments 4, 15 on fig.13).
Probably, to
resolve the problems of longitudinal fixing of approximating segments is
possible through the use of such curves (as the standards of the simplest
segments) which curvature will increase to their ends and is minimum in
the center (for example, curves of elliptic type). Apparently, approximation
of such type is capable to give objective (in our intuitive understanding)
subdivision of contour boundaries into pieces of minimum curvature, but
this problem demands the further researches.
The expediency
of further investigation in this direction as a whole is obvious. In
particular, legible longitudinal fixing of approximating segments essentially
would facilitate a solution of the subsequent problem of integral recognition-matching.
Obviously, the more precisely such fixing, the less final verifications
of standards of search objects with analysis pictures is required.
Despite of the some
successes, a final solution of the problem of longitudinal fixing of
approximating segments to obtain it was not possible. It was not possible
to fix, for example, these segments on lateral faces of an iron, and also
on a heel of an insole (see fig.13). Certainly it is possible to consider,
that these examples concern to some degenerated case - too smooth
curves. Nevertheless, in the exhibited examples basic unsteadiness
of the edge permitting to distinguish legibly a case when the contour
should be represented with an integral arc and when - composite one (namely
as the approximating segments should place in a true case on the
contour) is shown. Depending on initial approximations, random interferences,
and also not perfecteness of the form of objects themselves can
obtain various representations - subdivisions - of the contour lines corresponding
to identical elements of observation objects.
This situation
is aggravated also with that in practice a full detection of the contour
boundaries meets rather seldom. Only scraps of lines are
selected. The blacked out pieces (or superlighted) are badly reflected.
Some pieces can be absent basically, - owing to the possible partial overlapping
by other objects. The last circumstance represents one of the most characteristic
peculiarities of a solution of the problem of object recognition in actual
conditions. Generally, the approximating segments are not fixed on the
defined places basically.
All these circumstances
induce to do a conclusion about necessity to build-up the procedures
of integral pose matching in the supposition of a possibility of sliding
of approximating segments on the contour boundaries of the search objects.
Speculations in this occasion as the whole lead to a conclusion that the
separate segment of the simplest form (with feebly marked changes
of curvature), inherently, legibly defines the passing contour only in
the cross direction. Often to understand finally the longitudinal fixing
it is possible only proceeding from integral models of search contour
figures.
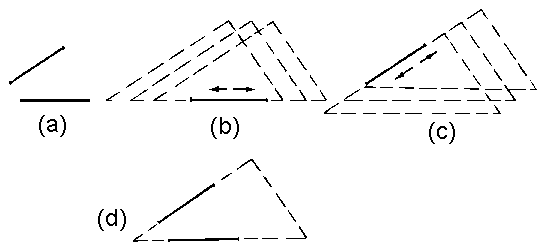
Fig.18 illustrates
this position for the simplest cases, particularly, - an incomplete
detection of rectilinear contours (fig.18a).
|
| Fig.18a,b,c,d |
Here the chosen
segments correspond to an angle of some figure. This angle can slide
concerning each of the chosen segments (fig.18b,c), and only the combination
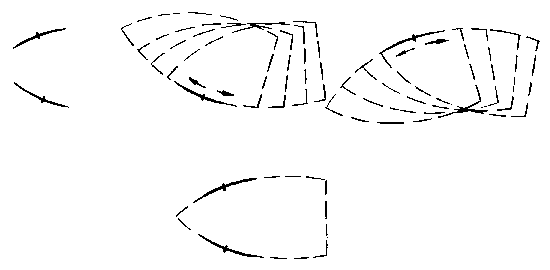
of such segments catches this angle legibly (fig.18d). The similar
example for a curvilinear angle (iron), which for example, is fixed
at least by two approximating (contiguous) segments (and by that defines
these segments as the defined parts of a contour of the search object),
is represented on fig.18e.
|
| Fig.18e |
Naturally, at the
so poorly fixing - fuzzy - primary-elementary matching of contours the
solution of the integral positional matching problem represents a nontrivial
problem. In this case, the separate segment generates as possible all
those positions of the search object, at which its standard contour is
only juxtaposed with this segment in the cross direction. To choose a
search position among so extensive set generated by each segment of an
observed picture is rather uneasy.
The following
stage of the given work also has been devoted to a solution of this problem.
At this stage the method [19] interpreting
the positional detection problem as accumulation of hypotheses [3], which in the case of objects defined - fixed
- forms allows to solve costructively the positional detection problem in
conditions of sliding primary-elementary matching of contours has been
developed.