The bell-like (fuzzy) assignment function is applied to solve the problem of the interference defended segmentation - approximation of the arbitrary shaped (curvilinear) contours.Vladimir I. SHULGA Ph.Dr., Senior Research Scientist, National Academy of Sciences of the Ukraine, Kiev .
E-mail: shulga@altavista.net
ABSTRACT
Whole recognition (singling-out) of the contour samples is realized with help of the accumulation of hypotheses about their parameters that are generated independently by separate primary signs (segments) singled out on the analyzed picture.
Index Terms (Key Words) - computer vision, image analysis; segmentation, approximation of contours, recognition (singling-out) of samples.
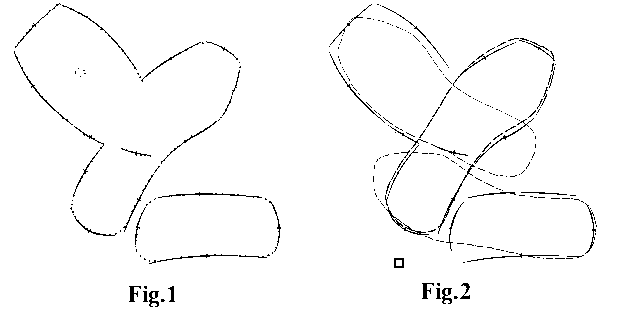
1. INTRODUCTIONThe represented procedural sequence solves the problem of recognition (singling-out) of non-complicated contour objects of an arbitrary shape with respect to their samples in presence of any other objects and when the sought ones are partially overlapped. Figure 1 and Figure 2 illustrates the start and final stage of the problem being solved.

This procedural sequence is based on:
1) the interference defended method of segmentation-approximation of contour boundaries;
2) the general-purpose method for description of the contours of an arbitrary (curvilinear) form within the terms of the segments of any standard form;
3) the fast manner for account of the integral verification of the contour samples.
The paper represents the base concepts (Section 2) and main peculiarities of the realization (Section 3) of these methods. Its details has been described in [1].
2. MAIN CONCEPTS2.1. One of the key problems of the approximation of the real contours is the choice of the allowed deviation of the contour points from the axis line of the approximating segment. The choice of this deviation must satisfy conflicting requirements. To avoid a false deviation of the approximating segment caused by interfering points, this value must be less as far as possible. Also it’s necessary that corners of the contours are analyzed shouldn’t be skipped (planed). On the other hand, the allowed corridor must be not very narrow, so that the accidental deflection of the contour points will not be received as signals for the false subdividing of the approximating representation.
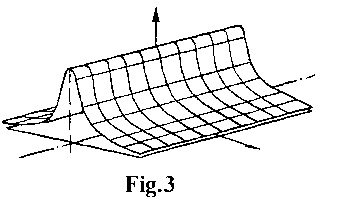
To relax this conflict one should leave conception of the threshold (“rude jumping”) points belonging and go to its “soft” (fuzzy [2]) estimation. Namely, the function of assignment of contour points to a separate segment should have the bell-like form (Fig.3). This function is the smooth symmetrical function tending to zero when the deviation from the approximating segment axis increases.
If such kind of the assignment function is used, this also lets (simultaneously with singling-out of subsets of the contour points that belong to separate segments) to solve the problem of approximation of these sets as the problem of maximization of estimation of the degree in which the approximating segments are verified by the contour points.
Such operative unity (which unites approximation with gently extraction) enables to avoid a false leading away of the approximating segments, their false subdividing and planing of the contour corners by this segments.
2.2. The main peculiarity of the representation of the arbitrarily shaped contours as the group of separate segments is essential absence of the legible ends of some line segments. Here one should operate with the linear elements that have fuzzy ends. The function estimating the degree of assignment of contour points to this element must have the bell-like form in longitudinal direction too (Fig.4).
Such function permits to rest on the length of the contour lines in proper way and for a maximum when they are approximated by the curves of some standard type (in the most rigid degree in centre, with gradual weakening in the periphery direction, according to their gradual divergence). In the present work the curves of the simplest type are used as the axial lines of the approximating segments, so they are the central part of the parabolas each branch of which may have its own curvature and “fuzzy length” (see Section 3.1.). Such segments are called contiguous (because their branches have only a “contiguity” with the approximated contours in general). Figure 1 shows the result of representation of the contour picture with such segments (here the thickness of each segment is reduced in the periphery direction in accordance with drops in its “distinctness”)
The contiguous (fuzzy end) segment conception application makes it possible to obtain the description of contour boundaries by means of the maximally stretched and, therefore, maximally stable standard linear elements. Here singling-out of such elements is the essentially simpler problem than the next one associated with recognition-matching of contour objects as a whole. When considering this aspect, it is possible to speak about the highly possible (optimally maximum) complicacy of the description of contour boundaries within the framework of the segments with fuzzy ends as the basis for further integrated recognition-matching of the contour objects of arbitrary shapes.
2.3. Complicacy of solution of the arbitrary-shape object recognition problem consists in that in general case of smooth contour boundaries it is in principle impossible to fix approximating segments in efficient way in definite places of the contours that are matched. The problem of elaboration of the constructive procedure which can choose the model image of an object that corresponds to the observations, under such fuzzy (sliding) primary segmental representation of contours is a rather non trivial issue.
When the sought objects are the figures of the definite fixed shape, the problem of the recognition such object can be solved constructively by way of accumulation (vote-count) of hypotheses about parameters of the objects and by registration of the hypotheses that are independently generated by the highest number of primary facts-features. The role of such facts is played by the elements of the segmental representation of an initial picture. Each of these facts-segments generates a set of hypotheses about a possible position of the desired object in analyzed image. Here, the most probable fact position is defined by the maximum crossing - clustering of sets which correspond to different facts - segments. Thus, the recognition-matching problem can be solved under computational costs that are much lower than for the direct contour matching case.
In practice that approach lead to technique (see Section 3.2.) similar to the algorithms the majority of which goes back to the famous Hough transform [3], [4]. The proposed ontological approach to the object recognition enables to see the deep community of this algorithms. The seeing of this community makes it possible to simplify the logic of elaboration and extension of such technique in essence.
Moreover, and what is above all, the developed algorithm is based on application of the contiguous segments with the fuzzy ends which are the most characteristic (informative) and at the same time they are the universal units of initial generation of the hypotheses about the global parameters of the arbitrary curvilinear contour objects. It was the use of the initial units like described above that enabled us to draw the search performed according to the hypothesis accumulation principle up to the possibility of the constructive application in the problem of recognition of such objects.
3. REALIZATION OF THE BASIC CONCEPTS3.1. In this work, a bell-like assignment function is defined by one of the simplest analytical expressions for function of the such kind:
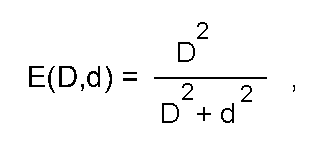
where:
d is deflection of the contour point from the axial line of approximating segments;Figure 5 shows the cross-section of the function under different D values. The interval [-D,+D] defines the assignment function width.D defines the deflection under which the assignment function is decreased twice;
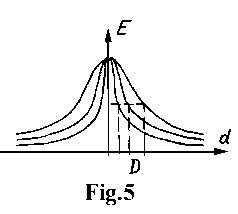
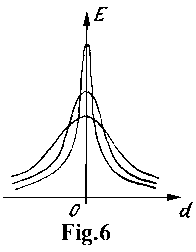
In addition, this expression is modified by reduction of the upper exponent from 2 to 3/2. In this case, the amplitude of the assignment function is increased if its width - D is decreased, but the branches of this function are dropped down under this decreasing, and otherwise (Fig.6). Such assignment function shape change character enable to construct a measure of segment verification which has sensitivity to the width of the approximated contour points subsets. (Similar technique also is applied to longitudinal direction.)
Taking into account all of told above the general mathematical expression for the such measure has the following form:
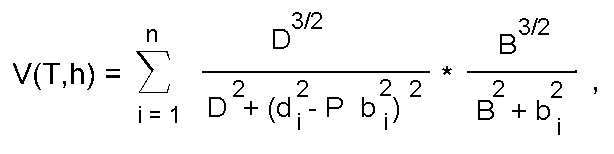
where
T is the set of counter points extracted from the image;b_i = (x_i - X)*½cos(A) + (y_i - Y)*½sin(A),n is the number of these points;
h = {X,Y,A,D,P1,P2,B1,B2}
are the parameters of the approximating segment;
X,Y are the coordinates of the segment centre, namely, its own coordinate system (Fig.7);
A is the segment slope;
D is the half-width of the assignment function;
P defines the curvature of the representing parabolas:
b_i, d_i are the parameters, defining the position of the contour point in own coordinate system (bOd) of the approximating segment; these parameters are found from the coordinates of the point:P1, if b_i >= 0 (right branch curvature),P2, if b_i < 0 (left branch curvature);
x_i, y_i with the transformations:
d_i = -(x_i - X)*½sin(A) + (y_i - Y)*½cos(A);
B defines the longitudinal deflection under which the assignment function is decreased twice (similar as D defines “twice decreasing” across deflection (B>>D)):Figure 1 shows the approximating segments which are defined by the parameters of the local maxima of this verify measure. The maxima are detected with the help of a gradient regulated-step procedure. The clearest elementary contour units are used as the initial approximations of the desired segments. These units are extracted by means of Hueckel operator [5]. In general, contour points are defined as the centers of all such units obtained in the tracing process of the brightness edges of the initial grey-toned images performed by this operator.B1, if b_i >= 0 (right branch length),B2, if b_i < 0 (left branch length).
3.2. The contour
shape recognition (singling-out) procedure was constructed under the consideration
that it is impossible to strictly fix approximating segments on the smooth
contours. The training part of this procedure imitates the moving of a
formal contiguous segment along contour boundaries of the standard of the
sought object (its separate full non-interfered image; see Fig.8).
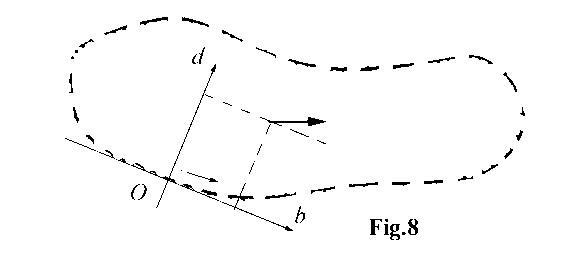
In this time, the standard’s position in respect to the own coordinate system of the sliding segment is determined on each step of this process (is determined position and orientation of an unit (basic) vector which has been fasten attached to the gravity center of the standard’s contour). The obtained set of the coordinate angle parameters is called as reference hypogram (because it is the record of the hypotheses about possible positions of the sought object).
At the stage of the recognition itself, this hypogram is sequentially juxtaposed to each of the contiguous segments were obtained after finishing the substage of the segmental representation of the contour picture that is analyzed. Under this juxtaposition, reference hypogram (its points) is translated in own coordinate angle system of this picture (here, the slope of the segment is added to the angle values).
The solution of the present recognition problem is defined with point (zone) of this system has been marked with largest amount of juxtaposed hypograms. This point determines such position of the object standard under which the contour of this standard is attached to largest amount of facts-segments.
Figures 9 and 2 illustrate the result of the recognition of the insole within the context of the contiguous segments represented on the Figure 1. Figure 9 depicts the comparative weights of all separate marked-rising points (zones) were registered in this experiment.
Figure 2 shows the positions of the object’s standard which are defined by first three of them. Black dashes correspond to the most marked-rising zones and the lighter ones to the next coming. (The program, which realizes the proposed algorithm, use the rectangular zone representation of space of the sought parameters. The relative shift size of one of these zones is shown on the left bottom on the Fig.2.)
4. SUMMARYWhen assessing the developed group as a whole we may say that here combined in some optimal way are the maximally rigid general-purpose primary matching of the arbitrarily shaped contours (the matching performed on the basis of their representation by the stretched segments with fuzzy ends), and, on the other hand, the method of integrated matching (hypotheses accumulation) which is able to constructively catch up the recognition process starting from this, although maximally rigid, but nevertheless sliding (“fuzzy”) method of primary matching of contours. And such link enabled to develop the interference defended constructively realizable procedure for recognizing of the objects having an arbitrary shape.
There are several directions for further elaboration of this work. First of all, it must be set to any modern living computer visual system. Technique of the computation can and must be essentially improved. Functional possibilities can be significantly extended.
Probability of future improvement of the proposed procedure group makes it possible to speak about the real plans of constructive extension of the presented approach also to more complicated situation (larger number of desired parameters), in particular, in order to perform recognition of 3D arbitrary shape objects of an arbitrary orientation.
Note that the proposed general-purpose interference defended arbitrary form contour segmentation-approximation may be useful not only within the framework of the developed recognition procedure sequence. It may be used as a stable basis for many contour analysis versions.
REFERENCES[1] V.I. Shulga, “Complex of Interference Defended Procedures of Contour Boundary Approximation and Recognition of Objects on Contour Images (research work)”/ Glushkov Institute of Cybernetics, Academy of Sciences of the Ukraine, Kiev, 1992, 75p. (in Russian)/ Deposited in All-Union Institute of Scientific and Engineering Information (Moscow), 04.01.92, N 12-B92.
[2] L.A. Zadeh, “Fuzzy sets”, Information and Control, 1965, N 8, pp. 338 - 353.
[3] P.V.C. Hough, “Method and means for recognizing complex patterns”, Pat. 3069654 (US), 1962.
[4] D.H. Ballard, “Generalizing the Hough transform to detect arbitrary shapes”, Pattern Recogn., 1981, Vol. 13, N 2., pp. 111 - 122.
[5] M. Hueckel, “A local visual operator which recognizes edges and lines”, JACM, 1973, Vol. 20, N 4, pp. 634 - 647.