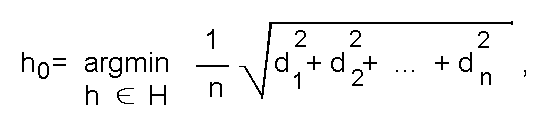
E-mail: shulga@altavista.net
КОМПЛЕКС ПОМЕХОУСТОЙЧИВЫХ ПРОЦЕДУР АППРОКСИМАЦИИ КОНТУРНЫХ ГРАНИЦ И РАСПОЗНАВАНИЯ ОБЪЕКТОВ НА КОНТУРНЫХ ИЗОБРАЖЕНИЯХ (исследовательская разработка)
Институт кибернетики имени В.М.Глушкова АН Украины, Киев.
Депонировано во Всесоюзном институте научной и технической информации (ВИНИТИ), Москва, 04.01.92, N~12-B92.
АННОТАЦИЯ
Описывается исследовательский комплекс, в основе которого лежат:
- помехоустойчивый способ разбиения-аппроксимации контурных границ, основанный на использовании колоколообразной (нечеткой) функции принадлежности контурных точек отдельному отрезку;
- универсальнный способ описания контуров произвольной (криволинейной) формы в терминах прилегающих отрезков - отрезков с нечеткими концами;
- методика распознавания объектов по принципу "накопления гипотез" об их параметрах, которые независимо порождаются отдельными первичными признаками, выделяемыми на анализируемой картине.
Последовательность процедур, построенных на этой основе, решает задачу распознавания (выделения) несложных контурных объектов произвольной формы по их образцам при наличии посторонних объектов и частичном перекрытии искомых. Приводятся результаты экспериментальной проверки, как всей последовательности процедур, так и ее отдельных компонент. Предлагаются пути их дальнейшего усовершенствования и распространения.
Представляет интерес для специалистов по обработке изображений, распознаванию образов, а также для специалистов, разрабатывающих проблемы зрительного очувствления манипуляционных роботов.
В В Е Д Е Н И Е
Настоящая работа посвящена исследованию и разработке методов помехоустойчивого представления контурных изображений в виде совокупности отдельных отрезков и последующего распознавания среди этих совокупностей отдельных объектов. Исследования проводились на контурных картинах, представляющих собой результаты выделения резких (скачкообразных) перепадов яркости на реальных полутоновых изображениях несложных сцен составленных из простых объектов.
В первом разделе рассматривается вопрос разбиения-аппроксимации реальных контурных линий. Показывается некорректность использования в решении этой задачи пороговой функции принадлежности. В реальных ситуациях, - когда контуры задаются дискретно и подвержены влиянию различных помех, следует использовать колоколообразную (нечеткую) функцию принадлежности контурных точек отдельному отрезку. Такая функция представляет собой гладкую симметричную функцию, стремящуюся к нулю при увеличении отклонения от осевой линии аппроксимирующего отрезка. При этом одновременно с выделением подмножеств контурных точек, принадлежащих отдельным отрезкам, решается и задача аппроксимации этих множеств как задача максимизации оценки степени подтвержденности аппроксимирующих отрезков контурными точками. Эта оценка вычисляется с помощью введенной функции принадлежности. Использование колоколообразной функции принадлежности позволяет корректно отстраиваться от посторонних точек, и, в целом, существенно повышает устойчивость процесса разбиения-аппроксимации реальных контурных границ.
Во втором разделе рассматриваются особенности решения задачи разбиения-аппроксимации контуров произвольной - криволинейной - формы. Принципиальная сложность представления таких контуров в виде совокупности отдельных отрезков заключается в том, что здесь не применимо такое понятие, как четкий конец отрезка, - здесь один отрезок плавно переходит в другой. В этом случае в настоящей работе предлагается оперировать линейными элементами, имеющими нечеткие - размытые концы. Функция, оценивающая степень принадлежности точек контура к такому элементу, должна иметь колоколообразную форму в продольном направлении. Такая функция принадлежности позволяет корректно, "по максимуму" опираться на длину контурных линий при их аппроксимации кривыми какого-либо стандартного типа (наиболее "жестко" по центру, с поcтепенным ослаблением к периферии, в соответствии с их постепенным расхождением).
Использование колоколообразной функции принадлежности позволяет получать описание контурных границ максимально протяженными, а потому - максимально устойчивыми стандартными линейными элементам. При этом, выделение таких элементов представляет собой принципиально еще более простую задачу, чем последующая задача распознавания-сопоставления контурных объектов в целом. В этом плане можно говорить об "оптимальности" описания контурных границ в терминах отрезков с нечеткими (размытыми) концами как базиса для последующего целостного распознавания-сопосталения контурных объектов произвольной формы.
В третьем разделе рассматривается вопрос целостного распознавания-сопоставления контурных объектов произвольной - криволинейной - формы. Сложность решения этой задачи состоит в том, что в общем случае, - случае плавных контурных границ, аппроксимирующие отрезки не фиксируются четко в продольном направлении. Каждый из таких отрезков может в принципе "скользить" по аппроксимируемым участкам (не от чего "оттолкнуться" - нет углов, - не на чем "остановиться" - нет четко выраженных минимумов кривизны). При этом, будучи принят в качестве элемента первичного представления анализируемой картины, такой отрезок порождает в качестве возможных соответствующее множество "скользящих" изображений искомого объекта. Задача построения конструктивной процедуры выбора "модельного" изображения искомого объекта, соответствующего наблюдаемой картине, среди этих множеств, представляет собой весьма не тривиальную проблему.
В случае, когда искомые объекты задаются эталонами определенной, фиксированной формы, эта задача может быть решена как задача поиска пересечения некоторых подмножеств точек пространства параметров, определяющих положение и ориентацию эталона на анализируемой картине. Точки каждого из этих подмножеств определяются возможными сопоставлениями эталона искомого объекта с одним из элементов "отрезочного" представления анализируемой картины. В случае плоских объектов, каждое такое подмножество представляет собой некоторую линию, отвечающую "скольжению" контура эталона по данному элементу (отрезку). Пересечение ("сгущение") максимального числа таких линий определяет пололожение эталона искомого объекта, порождаемое одновременно наибольшим числом "первичных" элементов (отрезков), - что и определяет решение задачи распознавания в данном случае.
В третьем разделе описываются особенности реализации процедуры распознавания объектов произвольной формы, построенной на базе этой методики. Приводятся результаты ее экспериментальной проверки. Предлагается теоретическое обобщение, интерпретирующее решение задачи распознавания таким способом как "накопление гипотез", порождаемых отдельными элементами наблюдаемой картины. Это обобщение наглядно демонстрирует суть предлагаемой процедуры распознавания, показывает ее связь с другими алгоритмами распознавания, и, в частности, с "классическими", основанными на непосредственной поэлементной проверке совпадения моделей искомых объектов с анализируемыми картинами (сравнение с эталоном). Проводится сравнение с ближайшим прототипом предлагаемой процедуры распознавания, а именно, с широко известными преобразованиями Хока (Hough).
Оценивая в целом предлагаемую процедуру распознавания, можно сказать, что в этой процедуре некоторым "оптимальным" образом сочетается "максимально жесткое" - универсальное первичное сопоставление контуров произвольной формы, а именно - сопоставление на базе их представления протяженными отрезками с нечеткими концами, а с другой стороны - метод целостного сопоставления - "накопление гипотез" - способный конструктивно "подхватить" процесс распознавания с этого, хотя и "максимально жесткого", но все же "скользящего ("нечеткого") способа первичного сопоставления контуров. Такая "связка" и позволила построить помехоустойчивую конструктивно реализуемую процедуру распознавания объектов произвольной формы.
Реализация предлагаемой процедуры рассчитана на работу с плоскими объектами. Рассматриваются возможности ее дальнейшего усовершенствования, позволяющие говорить о реальных перспективах конструктивного распространении предлагаемого подхода и на более сложные ситуации (с большим числом искомых параметров), в частности, для распознавания трехмерных объектов произвольной формы, находящихся в произвольной ориентации.
Материал разбит на 7 частей. Часть 1-я - ниже. Последующие - 2, 3, 4, 5, 6, 7.
1. АППРОКСИМАЦИЯ КОНТУРНЫХ ГРАНИЦ С ИСПОЛЬЗОВАНИЕМ КОЛОКОЛООБРАЗНОЙ ФУНКЦИИ ПРИНАДЛЕЖНОСТИ (БЕЛ-АППРОКСИМАЦИЯ)
Базовым этапом процесса анализа контурного изображения является его описание в виде совокупности отдельных "простейших" отрезков. Несмотря на свою кажущуюся простоту, практическое решение этой задачи представляет собой не тривиальную проблему. В реальных ситуациях, когда контурные границы задаются дискретным множеством точек, "искаженным" различными помехами, не удается решить задачу разбиения простейшим способом - по точкам скачкообразного изменения направления анализируемых контуров. Как правило, регистрируется множество "ложных" точек разрыва, обусловленных "неидеальностью" самой наблюдаемой предметной картины а также искажениями, вносимыми трактом преобразования изображений в цифровой вид. Приходится существенным образом опираться на процедуру аппроксимации (усреднения) анализируемых контуров некоторыми "модельными" отрезками.
Однако и на этом пути возникают серьезные затруднения. Рассмотрим их суть в контексте анализа особенностей решения задачи среднеквадратичной аппроксимации множества точек прямолинейным отрезком:
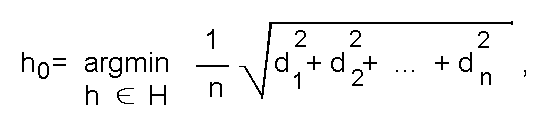
где
h - параметры, определяющие положение отрезка;
H - область допустимых значений параметров h;
n - число точек аппроксимируемого множества;
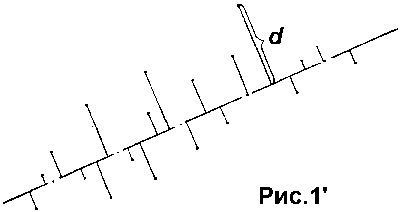
d_i - отклонение отдельной точки от осевой линии отрезка (рис.1').
Рассматриваемая задача, при заданном n в принципе эквивалентна следующей:
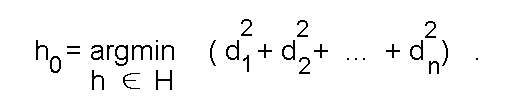
Эту задачу можно интерпретировать как задачу поиска минимума потенциальной энергии системы, состоящей из тонкого подвижного стержня, создающего вокруг себя некоторое поле, и неподвижных заряженных точек. В данном случае потенциал поля пропорционален квадрату отклонения от осевой линии стержня (рис.1а), а энергия определяется как сумма значений потенциала в этих точках.
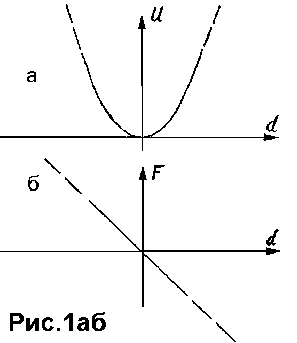
Суть этой задачи сводится к поиску положения, при котором силы, действующие на стержень со стороны точек, взаимно уравновешиваются. Эти силы определяются напряженностью поля, которая, в свою очередь, определяется скоростью убывания потенциала, т.е. величиной, обратной по знаку его производной. В данном случае, эта величина пропорциональна величине отклонения (рис.1б). Чем дальше точка от стержня, тем больше сила, с которой он ее к себе притягивает (и, естественно, наоборот).
В принципе так и должно быть - в основе задачи аппроксимации лежит "подтягивание" модели к удаленным точкам описываемого образа. Однако все это определяет желаемый результат, если аппроксимируемые точки лежат на своих истинных местах (определяемых формой модели) или разбросаны относительно последних интегрально симметрично. Иначе посторонние точки (принадлежащие, например, другим объектам) могут существенно исказить необходимый результат, "оттянув" аппроксимирующий отрезок на себя.
На рис.1" показан характерный пример применения (в "чистом" виде) процедуры аппроксимации к контурному изображению угла. По существу, в данном случае находится положение равновесия аппроксимируемого образа относительно аппроксимирующего отрезка. Можно сказать, что осевая линия этого отрезка "выводится" на центр тяжести аппроксимируемого множества (если рассматривать эту картину с точки зрения ее проекции на направление, перпендикулярное осевой линии).
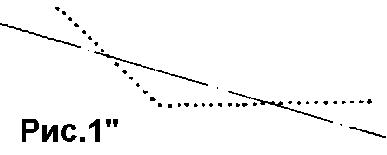
При этом, для того чтобы избежать "оттягивающего" влияния посторонних точек, обычно ограничивают область притяжения аппроксимирующего отрезка некоторым пороговым расстоянием (рис.1в). Однако такой способ ограничения влияния удаленных точек приводит к существенным затруднениям при построении устойчивых процедур аппроксимации реальных данных, так как в этом случае именно точки, обладающие наибольшей "притягательной" силой, оказывают скачкообразное влияние на положение аппроксимирующей модели.
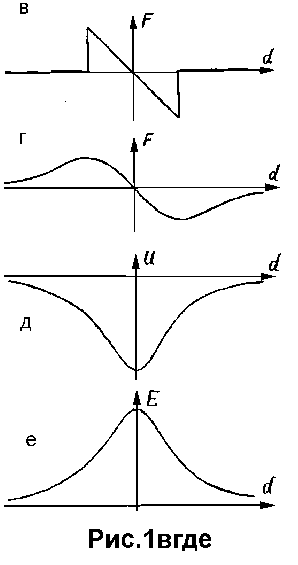
Кроме того, результаты процесса аппроксимации оказываются в целом очень чувствительными к выбору порога допустимого отклонения. Эксперименты показали (см., например, [1]), что при описании реальных контурных границ в терминах отрезков осевых линий невозможно однозначно подобрать порог допустимого отклонения, при котором одновременно не было бы ложного дробления аппроксимирующих отрезков, обусловленного случайными выбросами, либо срезов (усреднений) неярко выраженных углов анализируемых контуров.
Для того чтобы разрешить эти противоречия, естественно потребовать не порогового, а плавного ограничения влияния (притяжения) удаленных точек (рис.1г). Проинтегрировав такую плавную силовую функцию (со знаком минус), мы получим, что потенциал аппроксимирующего отрезка в данном случае должен представлять собой колоколообразную функцию (рис.1д). Минимизация суммы значений такого потенциала в заданных аппроксимируемых точках (т.е. минимизация суммарной потенциальной энергии) и дает искомое решение задачи аппроксимации, основанной на плавном ограничении влияния (притяжения) удаленных точек. Собственно в этом и заключается суть предлагаемого метода аппроксимации [2,3].
В соответствии с терминологией задачи распознавания величину, обратную этому потенциалу (рис.1е), будем интерпретировать как степень принадлежности контурных точек отдельному аппроксимируемому образу, а величину, обратную потенциальной энергии, - как функцию сходства этого образа с примеряемой моделью.
В наиболее общем виде предлагаемая постановка задачи аппроксимации некоторого множества точек отрезком линии выглядит следующим образом:1.1. Формальная постановка задачи
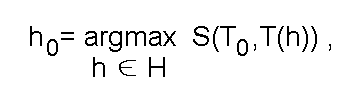
где
h - параметры, определяющие положение и ориентацию аппроксимирующего отрезка (в общем случае, и форму);
H - область допустимых значений параметров h;
T(h) - подмножество точек изображения, принадлежащих отдельному аппроксимирующему отрезку ("полоса" точек, окружающих его осевую линию);
T_0 - множество контурных точек, обнаруженных на изображении;
S - некоторая функция, определяющая меру сходства между
T_0 и T(h). В данном случае мера сходства вычисляется следующим образом:
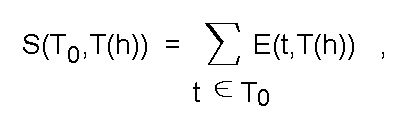
где E(t,T(h)) - функция, указывающая на степень принадлежности отдельной точки изображения t подмножеству T(h) (здесь подразумевается, что изображение определяется точками некоторой дискретной сетчатки, на которую оно проецируется).
Особенность предлагаемой меры сходства состоит в том, что при ее построении используется колоколообразная функция принадлежности. В дальнейшем наряду с этим термином будем также использовать термин "нечеткая функция", предложенный в [4] в качестве обобщающего названия для подобного рода функций. На рис.2а показан примерный вид такой функции для случая представления контурных границ прямолинейными отрезками.
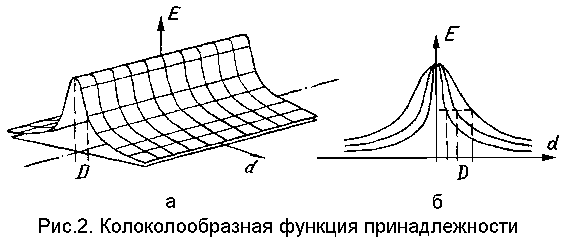
На рис.2б показано поперечное сечение семейства колоколообразных функций, определяемых одним из простейших аналитических выражений:
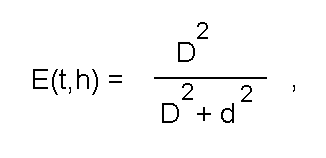
где d - величина отклонения от осевой линии аппроксимирующего отрезка, определяемого параметрами h; D - определяет отклонение, при котором значение функции принадлежности уменьшается в два раза (в дальнейшем удвоенную величину такого отклонения будем называть ее шириной).
При этом математическое выражение "нечеткой" меры сходства для случая представления контурных границ прямыми линиями определяется следующим образом:
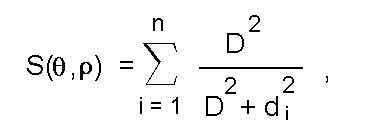
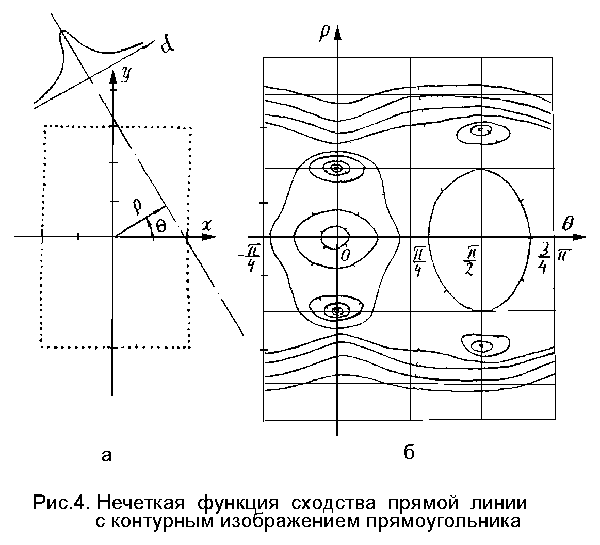
где teta, ro - параметры, определяющие положение осевой прямой (угол наклона и длина перпендикулярного к ней радиуса-вектора; рис.3а); d_i = x_i * cos(teta) + y_i * sin(teta) - ro (отклонение i-й контурной точки от осевой линии); x_i, y_i - координаты точки; n - число контурных точек. Здесь и далее в выражениях меры сходства будем опускать (подразумевая его присутствие) параметр To, обозначающий множество контурных точек.
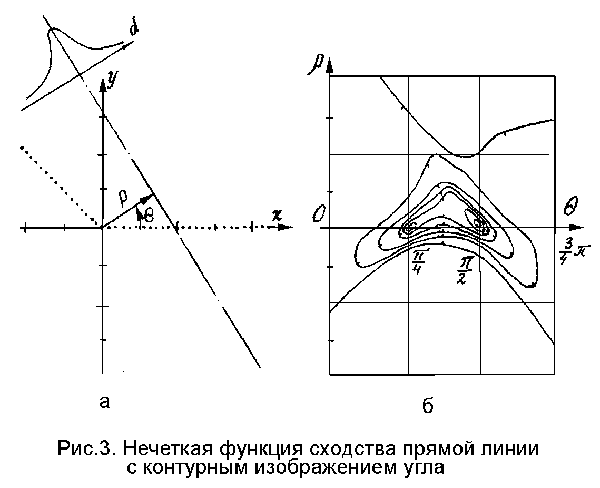
Задача аппроксимации здесь сводится к поиску локальных максимумов такой меры сходства, построенной с учетом всех контурных точек. На рис.3б показаны линии уровней этой функции для контурного изображения угла (рис.3а). Для того чтобы улучшить обозримость полученной картины (не "резать" максимумы по teta = 0), условно принимается, что длина радиуса-вектора может иметь отрицательное значение, что соответствует его наклону teta + pi. В верхней части рис.3а показан поперечный срез используемой функции принадлежности. На рис.4 показан аналогичный пример для контурного изображения прямоугольника. Как видно, каждому отрезку исходной контурной конфигурации здесь отвечает "свой" локальный максимум.