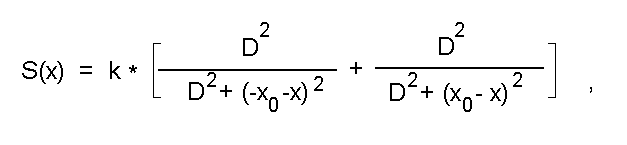
1. Оценка разрешающей способности бел-аппроксимации

Рассмотрим простейший случай двух параллельных отрезков, находящихся на расстоянии 2*x_0 друг от друга. На рис.5а показано поперечное сечение рассматриваемой картины. На этом рисунке положение осевой линии аппроксимирующего отрезка определяется параметром x. В данном случае

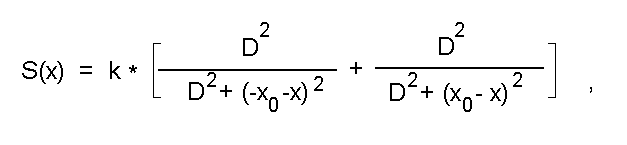
где k - число точек в каждом отрезке.

Экстремумы такой меры определяются нулевыми значениями ее производной:

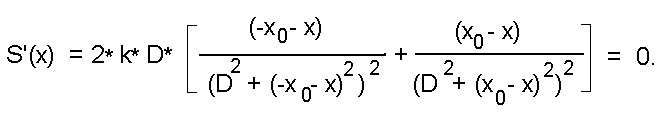
Знаменатель результирующего выражения положителен при любых значениях входящих переменных. Числитель можно преобразовать к виду

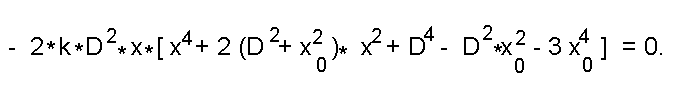
Это уравнение имеет пять решений, одно из которых x_1 = 0, и четыре других:

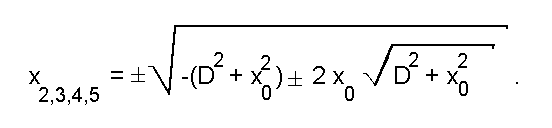
Два решения, соответствующих разности выражений, стоящих под знаком внешнего квадратного корня, имеют мнимые значения при любых значениях входящих переменных (так как x_0 > 0, по начальному соглашению - см. рис.5а). Два других имеют действительные значения, когда

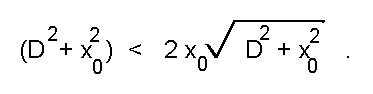
Упрощая это выражение, получим, что при D < sqrt3*x_0 исследуемая функция сходства имеет три экстремума: один центральный и два симметричных боковых. Нетрудно показать, что:

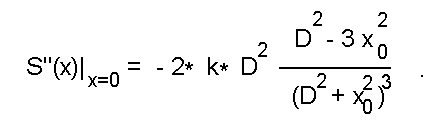
Очевидно, если D < sqrt(3)*x_0, то S"(x)|_0 > 0, т,e. центральный экстремум является локальным минимумом рассматриваемой функции сходства и, следовательно, соседние боковые - локальными максимумами этой функции (см. рис.5б). При D > sqrt(3)*x_0, эти максимумы сливаются в один (см. рис.5в). На рис.5г показаны положения максимумов в зависимости от значения параметра D (см. формулу для вычисления x_2...x_5).

2. К вопросу автоматической коррекции ширины функции принадлежности

Как утверждалось в разделе 1.3., максимум функции сходства, определяемого выражением

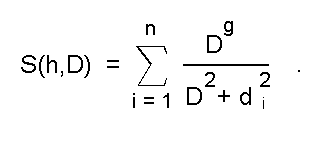
достигается при конечной величине параметра D, когда числитель этого выражения D\g (регулирующий скорость роста амплитуды), имеет показатель степени, лежащий в интервале 1 < g < 2.

Докажем это утверждение.

Будем рассматривать аппроксимируемый отрезок (см. рис.6б) как непрерывное множество точек. В этом случае мера сходства определяется интегралом

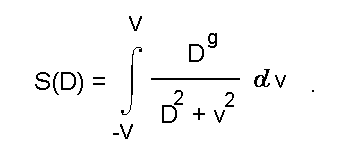
Здесь переменная v = d введена для того, чтобы избежать путаницы со знаком дифференциала. Поведение этой меры в зависимости от ширины функции принадлежности определяется ее производной по D:

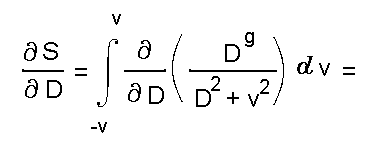
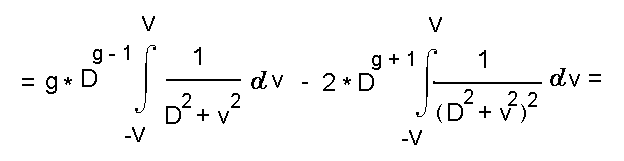
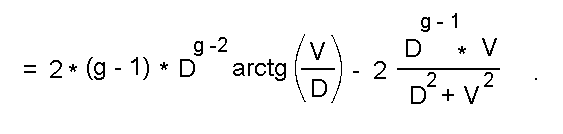
Приравнивая это выражение нулю, и вводя переменную gamma = V/D, получаем:

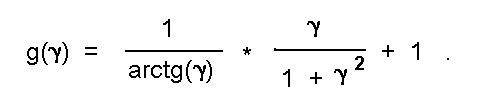
В интересующем нас диапазоне (0 < gamma < oo) эта функция имеет максимальное значение 2 при gamma= 0 и асимптотически приближается к единице при gamma -> oo (см. рис.6в). Монотонность ее убывания подтверждается тем, что ее производная всюду отрицательна на интервале 0 < gamma < oo:

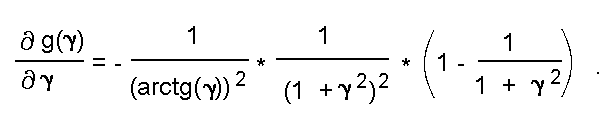
На рис.6г приведен график собственно интересующей нас обратной функции D/V = 1/gamma(g). Этот график показывает, какой будет ширина функции принадлежности (по сравнению с текущей относительной шириной аппроксимируемого отрезка) при достижении рассматриваемой мерой сходства своего максимального значения в зависимости от показателя g, регулирующего скорость роста амплитуды функции принадлежности.

3. Выбор величины шага пробных запусков процедуры представления контурных границ в терминах прилегающих отрезков

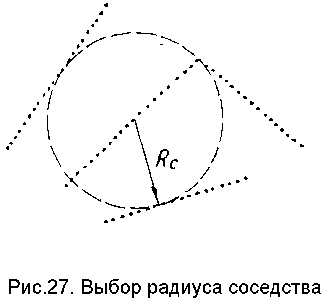
Предварительно оценивалась величина наименьшего радиуса соседств R_min среди радиусов соседств R_c всех контурных отрезков обрабатываемого изображения. Радиус соседства - это радиус наибольшей окружности с центром на данном отрезке, пересекаемой им и не содержащей точек других отрезков (рис.27).
 
 

Параметры X,Y начальных наборов отвечали узлам некоторой сетки на плоскости изображения, густота которой выбиралась так, чтобы в любую окружность радиусом R_min/2 попадал хотя бы один узел этой сетки (в случае квадратной сетки ее шаг должен быть меньше, чем R_min/sqrt(2)). Остальные параметры устанавливались одинаковыми для всех наборов. Величина параметра B, отвечающего длине начальных прилегающих отрезков, выбиралась меньшей, чем (R_min/2)*sqrt(3). Этот выбор обусловлен полученной теоретической оценкой для разрешающей способности предлагаемого метода аппроксимации. Параметр D выбирался равным 0.5 B, A - произвольным, P1 = P2 = 0.
 
 
 
 

4. Некоторые особенности организации процедуры поиска локальных максимумов нечеткой меры сходства

В ходе данной работы было опробовано несколько градиентных процедур поиска локальных экстремумов. Существенной особенностью этих процедур оказалось разворачивание системы координат, отвечающее смещению центральной точки аппроксимирующего отрезка вдоль хребтов функции сходства (характерный пример - процедура, описанная в [34]. Однако использование таких универсальных, а потому довольно громоздких процедур не оправдывает себя в ситуации, когда возможен предварительный учет специфики переменных, упрощающий поиск экстремума. Специфика переменных заключается здесь в четко выраженной их иерархии: в первую очередь подстраиваются угол и поперечное положение прилегающего отрезка, за ними - параметры ветвей, и только затем осуществляется движение в продольном направлении.

Такая специфика переменных позволила на втором этапе экспериментов эффективно использовать градиентную процедуру, в которой движение по всем переменным восьмипараметрической меры сходства осуществляется одновременно и в принципе независимо. В процессе поиска возможны задержки (пропуски шагов по некоторым переменным), если параметры с более высоким приоритетом еще не подстроились. В окончательном варианте использовалась следующая система приоритетов: (+,A), (P1,P2), (D), (B1,B2,

= ), где - "+" и "=" обозначают движения в поперечном и про- дольном направлениях соответственно. Шаг по какой-либо переменной увеличивается наполовину (с учетом ограничения на максимальную величину - см.далее), если он выполняется в том же направлении, что и предыдущий, и уменьшается в противном случае. При этом считается, что подстроились те переменные, шаг по которым стал меньше, чем 1/4 от величины максимально допустимого по данной переменной.

Последние величины выбирались из самых общих соображений так, чтобы в результате каждого шага новый аппроксимирующий отрезок не слишком выходил за границы старого. Шаги в продольном направлении (и по длине плеч) ограничивались величиной B/2, а в поперечном - D/2. Шаги по углу и кривизне не должны были колебать концы отрезка на величину большую чем D/2, т.е. detaA*MAX(B1,B2)/0.7 и deltaP*(B/0.7)\2 не должны превышать D/2. Во избежание проявлений дискретности задания анализируемых контуров величина параметра D ограничивалась снизу величиной, изменяющейся в диапазоне 0.5 - 2.5 расстояний между соседними точками растра. Сверху параметр D ограничивался величиной B/2.

Технически такие ограничения организованы так, что при подходе к одному из них следующий шаг разрешается делать только на половину расстояния до этого ограничения. Этим достаточно просто обеспечивается возможность увеличения шага при необходимости продвижения в обратном направлении. Начальные шаги по отдельным компонентам выбирались равными половине их максимально возможных величин. При этом начальные значения параметров B и D принимались равными 10 и 4 соответственно, а максимально допустимая величина шага по D равной 0.5. Процедура поиска очередного максимума меры сходства останавливалась, когда шаги по всем переменным становились меньшими, чем 0.2 их максимально допустимых величин.

Как правило, поиск максимумов, отвечающих контурным отрезкам, требовал в среднем 60 - 80 шагов по углу наклона и положению в поперечном направлении при 8 - 12 шагах в продольном направлении.

5. Некоторые детали реализации процедуры накопления гипотез

В программе, реализующей процедуру накопления гипотез, хранится информация только о помеченных зонах. Для этого отводится некоторый массив, запись в который делается с помощью L-хеширования [35] при котором ключом является номер зоны, а хеш-функцией - остаток от деления номера зоны на размер массива. В проведенных экспериментах этот массив состоял из 4096 ячеек. При этом начальный адрес поиска ячейки, отвечающей зоне с данным номером (хеш-функция), получался путем обнуления старших разрядов этого номера (начиная с 13-го). В каждой ячейке, кроме ключа зоны (номера в общем гипотетическом трехмерном массиве зон), хранится ссылка на описание данной зоны. Описание зоны - это также одна ячейка некоторого массива, в которой помечены биты, отвечающие номерам тех гипограмм, которые пометили данную зону. При этом пометка зоны отдельной гипограммой сводится к логическому сложению ее описания с ячейкой, в которой помечен бит, отвечающий номеру текущей гипограммы (массив таких ячеек заготавливается заранее). После окончания процесса пометки всеми гипограммами запускается операция преобразования содержимого каждого описания в число пометивших его гипограмм (для каждого описания - это одна машинная команда по подсчету единиц в данной ячейке).

При выполнении процедуры сглаживания номера окрестных зон не перевычисляются заново, а вычисляются путем сложения с добавками, переводящими номер центральной зоны в номер одной из 27 соседних зон (3х3х3). Эти добавки вычисляются заранее. Логика их вычисления определяется логикой вычисления общего линейного номера элемента (зоны) в многомерном (трехмерном) массиве.

Для того чтобы уменьшить число прилегающих отрезков, отслеживающих эталонный контур при построении его гипограммы, очередные точки эталонной гипограммы строятся по передней ветви последнего прилегающего отрезка. Можно сказать, что по этой ветви продвигается фиктивный касательный прилегающий отрезок, и в его системе координат регистрируются положения базисного вектора. Граница такого построения определяется рассогласованием положений базисного вектора в системах координат фактического и фиктивного отрезков. При этом шаг продвижения фактических отрезков непрерывно подстраивается с помощью обратной связи так, чтобы удержать величину рассогласования в пределах четверти зоны, а шаг фиктивных - чтобы удержать соседние точки эталонной гипограммы в пределах одной зоны. Под зоной, как и ранее, подразумевается элемент разбиения параметрического пространства. Если этого сделать не удается, то принимается, что в этом месте гипограмма имеет разрыв и ее построение продолжается с другого места контура эталона.

В последней версии программной реализации процесса накопления гипотез была предпринята попытка ограничить количество зон, участвующих в последующей процедуре сглаживания. Для этого выделялись так называемые районы пересечения, которые представляют собой совокупность зон, помеченных более чем двумя гипограммами, а также однократно помеченные зоны, непосредственно примыкающие к этой совокупности (соседство, как и ранее, ближайшее 3х3х3). Однако, несмотря на то, что, например, в описанном эксперименте время выполнения процедуры сглаживания в среднем сокращалось с 1.5 до 0.5 с, требовалось дополнительно около 0.5 с для выделения этих районов (при этом число анализируемых зон сокращалось в среднем в 5 раз). Возможно, эта процедура будет иметь существенные преимущества при более жестких ограничениях на вхождение в район пересечения. Естественно, что операция ограничения числа анализируемых зон имеет существенное значение при многократно повторенном сглаживании.

С П И С О К   Л И Т Е Р А Т У Р Ы

1. Шульга В.И. Программа, выявляющая простые многогранники на изображении сцены / Вопросы теории роботов и искусственного интеллекта. Киев : Ин-т кибернетики АН УССР. 1978. С.12-32.

2. Шульга В.И. Представление контурного изображения отрезками линий с помощью бел-аппроксимации / Математические и технические средства робототехники и распознавания образов. Киев : Ин-т кибернетики АН УССР. 1981. С.31-42.

3. Шульга В.И. Алгоритм обнаружения, определения положения и ориентации плоских объектов произвольной формы. Киев. 1984. 30с. (Препр. / АН УССР, Институт кибернетики им. В.М. Глушкова; N 84-41).

4. Zadeh L.A. Fuzzy sets / Information and Control. 1965. N8. P.338-353.

5. Хюккель М. Оператор нахождения контуров на кодированных изображениях / Интегральные роботы. М.: Мир, 1973. Вып.1. С.225-240.

6. Hueckel M. A local visual operator wich recognizes edges and lines / JACM. 1973. Vol.20. N4. P.634-647.

7. Дуда Р., Харт П. Распознавание образов и анализ сцен. М.: Мир. 1976. 512с.

8. Карапетян Г.К. Разработка, исследование и практическая реализация алгоритмов обработки и анализа графических изображений: Автореферат диссертации на соискание ученой степени кандидата технических наук. Киев. 1984. 24с.

9. Bellman R. On the approximation of curves by line segments using dynamic programming / Comm. ACM. 1961. Vol.4. N1. P.284.

10. Herman J., Tretiak O. A robust global edge detection algorithm / Proc. Intern. Conf. Cybern. and. Soc. 1979. P.147-150.

11. Montanari U. A note on minimal length poligonal approximation to a digitized contour / Comm. ACM. 1970. Vol.13. N1. P.41-47.

12. Ramer U. An iterative procedure for polygonal approximation of plane curves / Comput. Graph. and Image Process. 1972. N1. P.244-256.

13. Хоменок А.В. Универсальный фильтр для обработки яркостных и дальностных изображений // Математические и технические средства робототехники и распознавания образов. Киев: Ин-т кибернетики АН УССР. 1981. С.25-31.

14. Алгоритмы и программы восстановления зависимостей / Под ред. В.Н.Вапника. М.: Мир. 1984. 816с.

15. Браунли К.А. Статистическая теория и методология в науке и технике. М.: Наука. 1977. 408с.

16. Себер Дж. Линейный регрессионный анализ. М.: Мир. 1980. 456с.

17. Ивахненко А.Г. Самообучающиеся системы распознавания и автоматического управления. Киев: Технiка, 1969, 392с.

18. Merro L., Vassy Z. A simplify and fast version of the Hueckel operator of finding optimal edges in pictures / Proc. 4th, IJCAI. 1975. P.650-655.

19. Шульга В.И. Алгоритм поиска объектов на контурных изображениях / Распознавание образов и автоматизация проектирования робототехнических зрительных систем. Киев: Ин-т кибернетики АН УССР. 1982. С.12-24.

20. Pat. 3069654 (US) Method and means for recognizing complex patterns / P.V.C.Hough. 1962.

21. Обработка изображений при помощи неточечных преобразований / С.Л.Горелик, Е.Г.Михелевич, В.А.Пинцов, Л.А.Пинцов / Автоматика и телемеханика. 1979. N2. С.100-109.

22. Горелик С.Л., Пинцов В.А., Пинцов Л.А. Применение неточечных геометрических преобразований к распознаванию образов / Автометрия. 1975. N6. С.35-37.

23. Ballard D.H. Generalizing the Hough transform to detect arbitrary shapes / Pattern Recogn. 1981. Vol.13. N2. P.111-122. 24. Merlin P.M.,Farber D.J. A parallel mechanism for detecting curves in pictures / IEEE Trans. Comput. 1975. Jan. Vol. C-24. N1. P.96-98.

25. Stockman G. Object detection via image registration / Pattern recognition in practice. Amsterdam : North-Holland Publ. Comp. 1980. P.75-86.

26. Stockman G., Kopstein S., Benett S. Matching images to models for registration and object detection via clustering / IEEE Trans. on PAMI. 1982. Vol.4. N3. P.229-241.

27. Turney Jerry L., Mudge Trevor N., Volz Richard A. Recognizing partially occluded parts / IEEE Trans. on PAMI. 1985. Vol.PAMI-7. N4. P.410-421.

28. Розенфельд А. Распознавание и обработка изображений с помощью вычислительных машин. М.: Мир. 1972. 230с.

29. Sclansky J. On the Hough technique for curve detection / IEEE Trans. Comput. 1978. Vol.C-27. N10. P.923-926.

30. Гузман А. Разбиение визуальной сцены на трехмерные тела / Интегральные роботы. М.: Мир. 1973. Вып.1. С.241-262.

31. Уолтц Д. Интерпретация контурных рисунков, изображающих сцены с тенями / Психология машинного зрения. М.: Мир. 1978. С.30-111.

32. Бродская И.М., Камынин С.С. Алгоритм распознавания частично видимых объектов. Москва. 1980. 34с. (Препр./ АН СССР, Ин-т прикл. математики им. М.В. Келдыша; N 107).

33. Mckee J.W., Aggarwal J.C. Computer recognition of partial views of curved objects / IEEE Trans. Comput. 1977. Vol.1. N8. P.780-800.

34. Шор Н.З., Журбенко Н.Г. Метод минимизации, использующий операцию растяжения в направлении разности двух последовательных градиентов / Кибернетика. 1971. N3. С.51-59. 35. Кнут Д. Искусство программирования для ЭВМ. М.: Мир. 1978. Т3. Сортировка и поиск. 534с.
 

Вернуться
 

Конец. Возврат в начало.