| English |
1. БЕЛЛ-АППРОКСИМАЦИЯ.
1.2. - Подчеркивается общая некорректность – резкость обычного способа исправления этого недостатка посредством порогового ограничения величины допустимого отклонения.
1.3. - Предлагается использовать нечеткую - колоколообразную функцию для оценки степени принадлежности контурных точек к отдельному отрезку. Такая функция – белл-функция (от английского слова bell – колокол) представляет собой гладкую функцию, стремящуюся к нулю при увеличении отклонения от осевой линии аппроксимирующего отрезка.
1.4. - С ее помощью определяется мера общей – суммарной – нерезкой подтвержденности этого отрезка контурными точками. В итоге задачи разбиения контурной конфигурации на отдельные отрезки и их аппроксимации сводятся воедино – к поиску локальных максимумов такой меры. Вся эта методика в целом названа белл-аппроксимацией.
1.5. - Рассматривается место белл-аппроксимации среди процедур структурного представления линейных образов.
1.6., 1.7. - Даются общие рекомендации по определению главного параметра функции нечеткой принадлежности – крутизны ее скатов – ее ширины.
1.1,2,3. ФИЗИКА АППРОКСИМАЦИИ. ОРДИНАРНЫЙ СПОСОБ ФУНКЦИОНАЛЬНОЙ КОРРЕКЦИИ. СОДЕРЖАТЕЛЬНАЯ МОТИВАЦИЯ ПРОДВИНУТОЙ КОРРЕКЦИИ.
Множество методик, алгоритмов и процедур
анализа реальных данных базируется на минимизации среднеквадратического
отклонения. Среднеквадратическое приближение является классикой анализа
экспериментальных данных. Оно выравнивает - усредняет случайный
разброс регистрируемых данных. Определяет их главные - помехоустойчивые
характеристики. С его помощью подбираются обобщающие смысловые - геометрические
образы-модели.
Однако, среднеквадратическая аппроксимация, при неосторожном обращении,
может усреднить - обобщить, то что усреднять - обобщать в
принципе не следует. А именно, – не случайные – не статистические – «разовые»
помехи. Допустим, необходимо решить простейшую задачу аппроксимации множества
точек прямолинейным отрезком. При этом в поле зрения попали не только точки,
относящиеся к отдельному отрезку, но и точки соседнего. В подобном случае
мы получим бессмысленное усреднение - выравнивание угла секущей
линией – рис.1A.

|
|
Рис.1A |
Рассмотрим физическую
суть этого явления. Формальная постановка данной задачи определяется
следующим выражением:

где
| h
- |
параметры,
определяющие положение аппроксимирующего отрезка; |
| H
- |
область
допустимых значений параметров h; |
| n
- |
число
точек аппроксимируемого множества; |
| d_i
- |
отклонение
отдельной точки от осевой линии отрезка (рис.1B). |

|
|
Рис.1B |
Общий характер решаемой
задачи - положение искомых минимумов не изменятся, если опустить нормирующий
множитель 1/n, а также играющий подобную роль квадратный корень. Формальное
выражение упростится:

Эту задачу можно интерпретировать как задачу поиска минимума потенциальной
энергии физической системы. Система образуется множеством неподвижных заряженных
точек и тонким подвижным стержнем, создающим вокруг себя некоторое поле.
В данном случае потенциал поля пропорционален квадрату отклонения от осевой
линии стержня (рис.1a), а энергия определяется как сумма значений потенциала
в заданных точках.
|
|
|
Рис.1a |
Здесь наглядно иллюстрируется
физическая суть - основа задачи аппроксимации. Чем дальше точка отстоит
от осевой линии примеряемого образа, тем больше ее вклад в минимизируемый
функционал, - тем больше ее влияние на результат аппроксимации, - тем больше
сила, с которой эта точка притягивает аппроксимируемый обаз. В принципе так и должно быть. При
аппроксимации примеряемая модель должна подтягиваться к удаленным
точкам. Однако, все это дает желаемый результат только тогда, когда точки
аппроксимируемого образа находятся на своих местах (определяемых
формой модели) или разбросаны интегрально симметрично (в частности – по нормальному
закону). Иначе, посторонние точки могут существенно, а зачастую - фатально
исказить результат, оттянув аппроксимирующий образ на себя. Рис.1A
наглядно иллюстрирует это положение. Здесь осевая линия аппроксимирующего
отрезка выводится на центр тяжести аппроксимируемого множества,
- если смотреть на эту картину с точки зрения ее проекции на направление,
перпендикулярное к этой линии. Из физики ивестно - насколько сильно могут
увести этот центр даже небольшие, единичные, но далеко отстоящие "грузы"...
Для того чтобы избежать оттягивающего
влияния посторонних точек, обычно ограничивают область притяжения
аппроксимирующего отрезка некоторым пороговым расстоянием. Однако такой способ
ограничения влияния удаленных точек приводит к существенным затруднениям
при построении устойчивых процедур аппроксимации реальных данных. В этом
случае точки, обладающие наибольшей притягательной силой, оказывают
скачкообразное влияние на положение аппроксимирующей модели.
Результаты аппроксимации
оказываются весьма чувствительными к выбору порога допустимого отклонения.
На практике невозможно выбрать порог допустимого отклонения, при котором
одновременно не было бы ложного дробления аппроксимирующих отрезков, обусловленного
случайными выбросами, либо срезов (усреднений) неясно выраженных
углов анализируемых контуров. Результат применения среднеквадратичной аппроксимации
с пороговым ограничением допустимого отклонения [1]
демонстрируется на рис.10с. Здесь можно найти примеры обеих ситуаций. И
это лучшее, что можно было получить.

|
| Рис.10c |
|
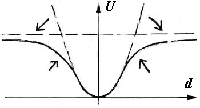
| Рис.1а_ |
|
|
| Рис.1b |
Силы, с которой поле действует на заряды, определяются напряженностью поля, что в свою очередь определяется скоростью падения потенциала. В данном случае напряженность обратно пропорциональна отклонению от осевой линии стержня,- производная от «x-квадрат» со знаком минус (рис.1b). Задача поиска минимума потенциальной энергии сводится к поиску положения стержня, при котором, действующие на него силы взаимно уравновешиваются. В нашем случае, - чем дальше точка от стержня, тем больше сила, с которой он ее к себе притягивает (и, естественно, наоборот).

|
| Рис.1c |
|
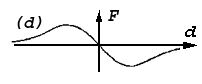
| Рис.1d |
|
|
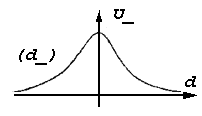
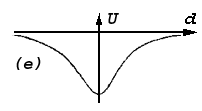
| Рис.1d_,1e |
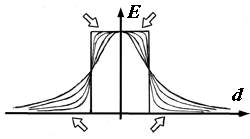
Покажем это. Проследим качественно процесc интеграции плавной силовой функции. Вначале, интегральная функция будет постепенно, с ускорением, возрастать (рис.1d_), в соответствии с монотонным увеличением абсолютной величины силы. Максимальная скорость возрастания – максимум крутизны интегральной функции, будет определяться максимумом – верхним пределом силовой функции. Затем скорость возрастания будет уменьшаться до нуля, – в точке перехода силовой функции через нуль. Потом, интеграл будет плавно падать, с ускорением, – максимум скорости падения отвечает нижнему пределу силовой функции. Затем, интегральная функция будет плавно, с замедлением, асимптотически приближаться к исходному нулевому значению. В целом получается колоколообразная зависимость (рис.1d_).
Потенциальная функция получается из полученной путем ее инвертирования (рис.1e). Делается это потому, что потенциал падает в направлении силы, поэтому при интегрировании ее значение необходимо брать со знаком минус, или потом инвертировать результат (что было выбрано для большей наглядности процесса интегрирования). Суммарная потенциальная энергия системы теперь оределяется как сумма значений такого потенциала в заданных аппроксимируемых точках. Минимизация этой - суммарной величины и дает искомое решение задачи аппроксимации, основанной на постепенном ограничении влияния (притяжения) удаленных точек.
Привлечение силовой – дифференциальной интерпретации позволяет более четко сформулировать задачу и объяснить суть ее решения. Вместо рассуждений о некотором потолке определяется, что сила действия должна стремится к нулю при увеличении отклонения. Силовая интерпретация более строго объясняет и аппроксимирующую роль центрального участка потенциальной кривой (остатка параболы - потенциальной ямы). Вместо (в дополнение) рассуждений о том, что точки должны скатываться на ее дно, - здесь дается непосредственное представление о действующей на них силе – обратно пропорциональной отклонению, с изменением знака при переходе через нуль. Логически проще в рамках силовой интерпретации связываются среднеквадратичная аппроксимация и пороговое ограничение порога допустимого отклонения (рис.1с).

|
| Рис.1f |
|
| Рис.1f_ |
В наиболее общем виде предлагаемая постановка задачи аппроксимации некоторого множества точек отрезком линии выглядит следующим образом:

где
| h
- |
параметры, определяющие
положение и ориентацию аппроксимирующего отрезка (в общем случае, и форму); |
| H
- |
область допустимых
значений параметров h; |
| T(h)
- |
подмножество
точек изображения, принадлежащих отдельному аппроксимирующему отрезку (некий
идеальный образ этого отрезка, - "полоса" точек, окружающих
его осевую линию); |
| T_o - | множество контурных
точек, обнаруженных на изображении; |
| S - | мера геометрического
подобия ~ сходства ~ соответствия (conformity) множества (образа) T(h) и множества T_o. |
В данном случае эта мера вычисляется следующим образом:

где E(t,T(h)) - функция, указывающая на степень принадлежности отдельной точки t подмножеству T(h) (здесь подразумевается, что изображение определяется точками некоторой дискретной сетчатки, на которую оно проецируется).
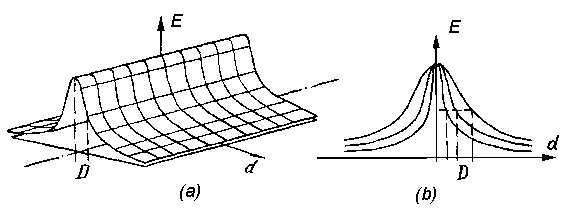
Особенность предлагаемой меры геометрического подобия - сходства состоит в том, что при ее построении используется колоколообразная функция принадлежности. На рис.2а показан примерный вид такой функции для случая представления контурных границ прямолинейными отрезками.
|
| Рис.2 |
В данной работе использовалось одно из простейших
аналитических выражений для такого рода функций:

где
| d
- |
величина
отклонения от осевой линии аппроксимирующего отрезка, положение которого
определяется параметрами h; |
| D
- |
определяет
отклонение, при котором значение функции принадлежности уменьшается в два
раза (в дальнейшем удвоенную величину такого отклонения будем называть
ее шириной). |
Поперечное сечение семейства колоколообразных функций,
определяемых этим выражением показано на рис.2b.
В дальнейшем наряду с термином колоколообразная
будем также использовать термин нечеткая, предложенный в [4] в качестве обобщающего названия для подобного
рода функций.

где
| h
– |
параметры,
определяющие положение аппроксимирующего отрезка, |
| T_o
- |
множество
выделенных контурных точек, |
| d_t
- |
отклонение
точки-t от аппроксимирующего отрезка. |
Для случая аппроксимации прямыми линиями эта мера
определяется следующим образом:

где
| наклон
перпендикулярного радиуса-вектора, опущенного из центра координат на аппроксимирующую
линию (рис.3a), |
|
| длина
этого вектора, |
|
| d_i - |
отклонение
i-той контурной точки от осевой линии = x_i * cos( |
| x_i, y_i
- |
координаты точки, |
| n
- |
число
контурных точек. |
Здесь и далее в выражениях меры сходства будем опускать (подразумевая его присутствие) параметр T_o, обозначающий множество контурных точек.
|
| Рис.3 |
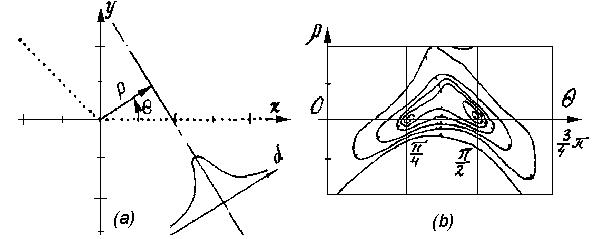
Задача аппроксимации сводится к поиску локальных
максимумов такой меры, построенной с учетом всех контурных точек. Линии уровней
этой меры (функции), для контурного изображения угла (рис.3a), показаны
на рис.3b. Для того чтобы улучшить обозримость полученной картины (не резать
максимумы по ![]() = 0), условно принимается, что длина радиуса-вектора может иметь отрицательное
значение, что соответствует его наклону
= 0), условно принимается, что длина радиуса-вектора может иметь отрицательное
значение, что соответствует его наклону ![]() + pi. В нижней части рис.3a, показан поперечный срез используемой функции
принадлежности.
+ pi. В нижней части рис.3a, показан поперечный срез используемой функции
принадлежности.
Как
видно, каждому отрезку исходной картины здесь отвечает свой локальный максимум
"мягко выделяющей" меры геометрического сходства.
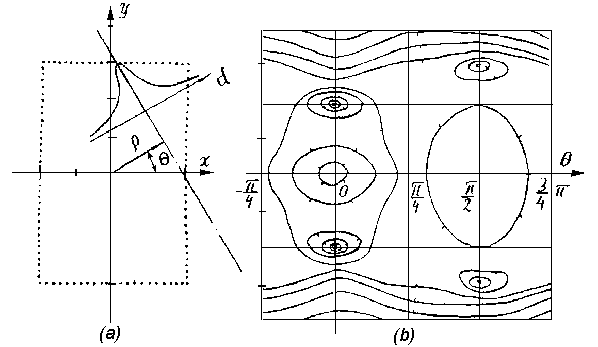
Аналогичный пример для контурного изображения прямоугольника
показан на рис.4.
|
| Рис.4 |
В дальнейшем, мера сходства, построенная на основе колоколообразной функции (bell-function) принадлежности будет также называться белл-сходством (bell-conformity), аналогично тому как процедура поиска его максимумов - белл-аппроксимацией (bell-approximation).
Естественно, поиск локальных максимумов меры геометрического сходства, основанной на использовании колоколооюразной функции принадлежности, представляет собой принципиально более сложную задачу, чем классический поиск минимума среднеквадратичного отклонения. Это определяется простотой параболы по сравнению с колокольчиком. В частности, для аппроксимации прямыми линиями существует аналитическое решение. Одним из примеров аналитического решения задачи нахождения минимума среднеквадратичного отклонения является оператор Хюккеля [5, 6], используемый и в данной работе для нахождения элементарных контурных перепадов на полутоновых изображениях. Кроме того, известно, много случаев эффективной реализации процесса нахождения максимумов взаимной корреляции для различного вида образов (при этом, по существу, ищется минимум среднеквадратичного отклонения [7]).
Поэтому в целом естественно желание остаться, по возможности, в рамках решения задачи нахождения минимума чистого среднеквадратичного отклонения.
Однако, минимум стандартного отклонения, как уже отмечалось, по своей сути отражает глобально-усредненное сходство модели (примеряемого образа) с анализируемым образом. В этом случае мера сходства монотонно убывает с увеличением отклонения любого элемента анализируемого образа от соответствующего элемента примеряемой модели.
Получить адекватное описание какой-либо картины с помощью такой меры сходства можно только в случае, когда среди сопоставляемых моделей присутствует модель всего анализируемого образа. В этом случае, минимизируя суммарное отклонение, мы можем получить искомый результат, т.е. найти соответствующую модель. Иначе мы получим усреднение анализируемого образа одной из имеющихся моделей, что может не иметь ничего общего с необходимым результатом - адекватным описанием данного образа или хотя бы его части.
Эффективность использования критерия суммарного (среднеквадратичного) отклонения непосредственно зависит от того, насколько четко мы можем выделить аппроксимируемый образ из его окружения, либо насколько полно мы можем отразить анализируемую картину какой-либо целостной моделью. С этой точки зрения можно выделить два подхода в решении задачи описания картин различного вида на основе минимизации среднеквадратичного отклонения:
- последовательное независимое выделение и аппроксимация отдельных образов, входящих в состав анализируемой картины [1, 5, 6, 13], в частности, отдельных отрезков контурных границ.
- аппроксимация исходных данных целостными моделями
(см., например, [8 - 12]), в частности, контурные
границы - цепочками отрезков;
Адекватность анализируемым картинам представлений, получаемых на основе последнего подхода, обеспечивается в первую очередь тем, что здесь элементы (точки) исходных данных в итоге будут распределены между соответствующими элементами (отрезками) примеряемых моделей и не будут оказывать столь негативного оттягивающего влияния на смежные элементы (отрезки) примеряемой модели. Например, если аппроксимировать угол (см. рис.1A, рис.3) соответствующей целостной моделью (цепочкой из двух отрезков), то, в принципе, можно получить адекватный результат даже в рамках чистой стандартной аппроксимации.
Однако такой подход эффективен только как подстроечный, когда априори имеется первичное приближение - модель уже достаточно хорошо отражающая анализируемую картину, - модель, которую остается только подстроить. Прерогатива определения таких первичных моделей остается за первым подходом - последовательным контекстно-независимым выделением и аппроксимацией отдельных подобразов.
В решении этой задачи, в свою очередь, также можно выделить два подхода, в зависимости от способа выделения элементов принадлежащих отдельным подобразам:
- априорное выделение - неуправляемое примеряемыми моделями в процессе аппроксимации [5, 6, 13];
- выделение управляемое в процессе аппроксимации (см., например, [1]), - отбрасывание элементов, находящихся вдали от соответствующих элементов примеряемой модели.
Достоинством первого подхода заключается в том, что при его применении среднеквадратичное приближение используется в своем чистом виде, с вытекающей отсюда вычислительной простотой. Однако, такой подход может быть использован только для представления анализируемых картин простейшими - элементарными образами. Эти образы должны достаточно адекватно представлять любой произвольно выбранный участок описываемой картины (во всяком случае, - большинство таких участков). Такое требование может быть удовлетворено только для представления в терминах простейших образов, находящихся на уровне дискретности задания исходных данных. Для изображений такими элементами являются участки размером в несколько точек растра (порядка 5 - 10). Только на таких участках, контурные границы с достаточной точностью могут быть описаны прямолинейными отрезками - простейшими универсальными образами, в терминах которых в принципе может быть описана произвольная контурная конфигурация.
Достоинством второго подхода является возможность работы с протяженными образами, дающими более осмысленное описание анализируемых картин. Однако в этом случае существенно усложняется техника решения задачи аппроксимации. Задача становится многоэкстремальной, требующей в принципе для своего решения использования начальных приближений, получаемых вне этого подхода. Кроме того, обычное использование при этом пороговой функции принадлежности приводит к неустойчивости процесса аппроксимации...
И если задача выбора начальных приближений в принципе решается на основе первого подхода, - выделения простейших образов, то проблема некорректности порогового отбрасывания посторонних точек до сих пор практически не решалась.
Именно здесь играет свою решающую роль колоколообразная (нечеткая) функция принадлежности. Замена пороговой функции на колоколообразную, при построении меры сходства аппроксимирующих моделей (отрезков) и описываемых данных (контурных границ), позволяет ослабить критичность при определении принадлежности элементов исходных данных к отдельному аппроксимируемому образу. Колоколообразная функция принадлежности сглаживает разрывы функции сходства, обусловленные дискретностью представления контурных границ, а также случайными помехами, что позволяет применять простые градиентные процедуры при поиске ее экстремумов. Кроме того, расширение оснований искомых максимумов (обусловленное ветвями колоколообразной функции принадлежности) обеспечивает меньшую критичность в выборе начальных приближений. Эксперименты (в том числе и на реальных изображениях) подтвердили справедливость этих положений (см. раздел 2.2.).
В целом, анализ особенностей различных подходов в решении задачи аппроксимации контурных границ приводит к выводу о целесообразности их комплексного, последовательного использования. В начале, с помощью процедур чистой среднеквадратичной аппроксимации контурное изображение можно описать в терминах простейших линейных элементов. Затем, наилучшие из них (определяемые минимальными значениями величины отклонения) - использовать в качестве начальных приближений для последующей процедуры максимизации "мягко выделяющей" меры сходства, получая в результате описание протяженными отрезками. После чего, в случае необходимости, можно подстраивать параметры этих отрезков как целостной совокупности, перераспределяя контурные точки между ними.
В заключение этого раздела следует остановиться на общих методологических достоинствах концепции колоколообразной - нечеткой - функции принадлежности. В принципе, в задаче описания реальных контуров, возможно применение вероятностных оценок принадлежности контурных точек к отдельному образу [14, 15, 16]. Однако, как показывают эксперименты, лежащая в основе этого подхода статистическая модель контурных границ, в которой сигналы представляют собой прямоугольные перепады (идеальные отрезки), искаженные нормальным шумом, является теоретической идеализацией, весьма далекой от действительности. Реальные искажения контурных границ - это различные искривления, пятна, вырывы и т.п., учет которых в статистических моделях вызывает существенные затруднения, и отвлекают от сути решаемой задачи. Суть этой задачи в данном случае заключается в выведении аппроксимирующего отрезка на осевую линию представляемого участка контурных границ, с корректным ограничением влияния посторонних точек.
Решение задачи описания контурных границ в терминах отрезков осевых линий как задачи поиска максимумов белл-сходства, с постулированием нечеткой - колоколообразной функции принадлежности, представляется более плодотворным, чем конструирование строгих моделей исследуемых сигналов. При этом относительно этих сигналов предполагаются только самые общие свойства, а именно - значительная разреженность множества отрезков линий, каждый из которых может быть искажен отдельными выбросами, искривлениями и т.п.
Сказанное выше можно дополнить утверждением, высказанным
в работе [17]: "...убеждение многих исследователей
в том, что теория статистических решений дает какую-либо более строгую и
объективную классификацию, чем другие алгоритмы принятия решений, является
формалистическим заблуждением...объективной меры (близости) нет в силу субъективного
характера постановки задачи распознавания образов...более важным, по-видимому
является, вопрос о простоте определения меры близости (сходства) ...". Для
многих задач вполне достаточно использования концепции нечеткой (колоколообразной)
функции принадлежности и основанной на ее использовании меры геометрического
сходства, как, например, в рассматриваемом способе аппроксимации контурных
границ. При этом существенно упрощаются построение и модификация процедур
сегментации - аппроксимации.
Например,
совершенно естественно вводятся необходимые по ходу решаемой задачи изменение
ширины функции принадлежности и нечеткость (размытость) концов аппроксимирующих
отрезков (см. последующие разделы).
Одним из основных вопросов при использовании нечеткой функции принадлежности является выбор ее ширины. Очевидно, чем меньше ширина функции принадлежности, тем точнее результирующие осевые линии отвечают контурным отрезкам. Однако с уменьшением этой величины могут появиться побочные, локальные максимумы, обусловленные дискретностью представления и помехами, причем наиболее вероятно их появление вдали от основных (искомых) максимумов.
Получение каких-либо строгих аналитических оценок,
характеризующих эти явления в общем случае, представляется весьма сложной
задачей. Решающую роль здесь, очевидно, должны играть экспериментальные
исследования. В качестве приблизительных оценок можно использовать результаты
анализа простейшего случая, а именно случая двух параллельных отрезков.
Поперечное сечение данной картины показано на рис.5a. Положение отрезков
здесь определяется точками x0 и -x0, а положение осевой линии аппроксимирующего
отрезка определяется параметром x.

|
| Рис.5a
|
Аналитические исследования, проведенные на базе
предложенного выражения функции принадлежности, показали, что функция сходства
в этом случае имеет отдельные максимумы, отвечающие двум параллельным отрезкам,
если ширина функции принадлежности имеет величину, меньшую, чем расстояние
между этими отрезками, увеличенное в sqrt(3) раз (рис.5b).

|
| Рис.5b
|
Если это не так, то максимумы сливаются в один
(рис.5c). Доказательство этого утверждения приведено в Приложении 1.6.A.

|
| Рис.5c |
Положения максимумов в зависимости от значения параметра
D показаны на рис.5d. На этом рисунке, для того чтобы сохранить соответствие
горизонтальной оси предыдущим рисункам, независимая переменная D откладывается
по вертикальной оси. Погрешность оценки положения искомых отрезков по максимумам
рассмотренной меры сходства резко уменьшается с уменьшением ширины функции
принадлежности. Например, уже при D < x_0 не превышает 0.1 величины расстояния
между отрезками, а при D < 0.5*x_0 - 0.01 той же величины.

|
| Рис.5d |
Приведенные результаты аналитических исследований
позволяют оценить условия слияния соседних точек аппроксимируемых контуров.
При ширине функции принадлежности, превышающей шаг дискретности представления
исследуемых контурных отрезков более чем в sqrt(3) раз, функция сходства
будет иметь один общий локальный максимум для каждых двух соседних точек,
даже при перемещении аппроксимирующей линии перпендикулярно к отрезку,
соединяющему эти точки.
В целом представляется естественной организация процесса поиска локальных максимумов белл-сходства, при которой ширина функции принадлежности изменяется в процессе поиска. Вначале следует задавать ее достаточно большой, обеспечивающей только разделимость отрезков, а затем уменьшать ее в соответствии с уменьшением рассогласования между осевой линией и представляемым контурным отрезком. Такая организация процесса должна обеспечить высокую точность оценки положения контурных отрезков и при этом уменьшить вероятность нахождения ложных максимумов. В этом случае начальную ширину можно выбирать весьма приблизительно, руководствуясь простейшими полученными оценками для разрешающей способности белл-аппроксимации.
Коррекцию функции принадлежности предлагается осуществлять путем непосредственного введения ее ширины в число искомых параметров меры сходства и использования такой функции принадлежности, у которой амплитуда при уменьшении ее ширины возрастает (рис.6a):
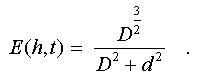
|
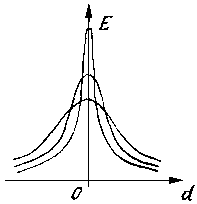
|
| Рис.6а |
В итоге, выражение, определяющее меру сходства приобретает следующий вид:

В этом случае при каждом фиксированном наклоне осевой линии локальный максимум такой меры достигается при D = 0.7*V, где V - относительная полуширина представляемого отрезка (половина длины его проекции на направление, перпендикулярное к текущему направлению осевой линии, рис.6b).
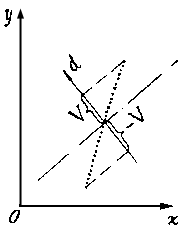
|
| Рис.6b |
В процессе поиска очередного максимума такого сходства
с уменьшением рассогласования между представляемым отрезком и осевой линией
будет соответственно уменьшаться и ширина функции принадлежности, обеспечивая
тем самым необходимую точность определения положения отрезка. Такая мера
сходства чувствует относительную ширину отрезка. Это связано с тем,
что теперь при увеличении ширины функции принадлежности одновременно с
увеличением вклада удаленных точек в значение функции сходства уменьшается
вклад точек, находящихся вблизи осевой линии. Причем равновесие между изменениями
этих вкладов наступает при конечной величине параметра D, когда числитель
в выражении для меры сходства D\g (регулирующий скорость роста амплитуды),
имеет показатель степени, лежащий в интервале 1 < g < 2 (рис.6c).
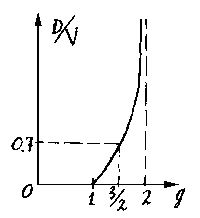
|
| Рис.6c |
Здесь показан график значений отношения D/V, при
которых мера сходства имеет максимальное значение в зависимости от параметра
g. Это утверждение доказывается в Приложении
1.7.A. В данной работе использовалось значение показателя степени g
= 3/2, что упрощает вычисления и приводит к устойчивому слежению за относительной
шириной отрезка. При этом, как уже отмечалось, D = 0.7*V.

